Упругость.

Благодаря упругой деформации осуществляется передача энергии от одной части тела к другой. Это свойство характеризуется модулем упругости (модулем Юнга) или модулем сдвига. Процесс передачи мощности по стержню при детальном рассмотрении является достаточно сложным.

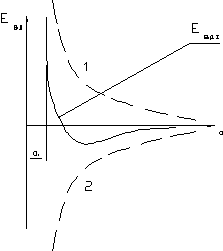
Силы связи в металлах определяются силами отталкивания и притяжения между ионами и электронами. Атомы располагаются на расстоянии, при котором энергия взаимодействия минимальна. Этому равновесному состоянию соответствует расположение атомов на расстоянии a_o (см. рис.2.5) .

Сближение или удаление атомов сопровождается совершением какой-либо работы. Из-за этого атомы в кристалле располагаются закономерно в правильных кристаллических решетках с минимальной энергией взаимодействия, которую называют энергией Гиббса.

При каком либо механическом воздействии, напряжения от которого не превышают предела упругости, атомы в кристалле сближаются или удаляются друг от друга. Однако после прекращения действия такого усилия расстояния между атомами восстанавливаются из-за стремления любой системы к устойчивому состоянию с минимальной энергией. Это свойство хорошо наблюдается при статических, т.е. не меняющихся нагрузках, и описывается законом Гука

s= Еq, (2-15)

где Е - модуль упругости; q - относительная деформация; s- напряжение в материале.

Рис.2.5.

Зависимость энергии взаимодействия Е_вд между ионами и электронами в кристалле:

1- силы отталкивания;

2- силы притяжения;

Е_вдå- суммарная энергия

взаимодействия.

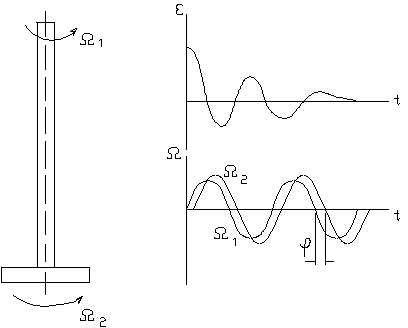
Рассмотрим передачу крутильных колебаний через металлический стержень (см. рис.2.6), как тело, представляющее собой сплошную среду.

Здесь ведущий конец вращается с угловой скоростью (частотой) W₁, а ведомый конец с маховиком вращается с частотой W₂ (рис.2.6,а). На рис. 2.6,б изображен возможный переходный процесс, когда ведущий конец жестко зажат, а ведомый конец с маховиком после закручивания на некоторый угол e отпускают, и он через нескольких колебаний опять успокаивается. На рис. 2.6,в показана реакция на гармоническое изменение W₁.

Из физики и сопромата известно, что угол закручивания ведомого конца равен

Da = M_крl/(GJ_p)= J_к W_p t= J_к М_кр, (2-16)

а максимальные касательные напряжения в сечении равны

t = М_кр / W_{p ,} (2-17)

 

 

б)

Рис. 2.6

Передача колеба-ний через метали-ческий стержень:

а) стержень с при-соединенным ма-ховиком;

б) переходный процесс в механиз-ме;

в) реакция на гармоническое воздействие.

а) в)

 

где М_кр - крутящий момент; l - длина стержня; J_к= 2l/(Gpr⁴)- коэффициент упругости; J_p, W_p - соответственно геометрические полярные момент инерции и момент сопротивления сечения стержня; G- модуль сдвига.

 

В динамике наблюдается несколько иное.

Запишем с учетом (2-16) уравнение моментов для стержня

C_кр(a₁- a₂)=М_кр+ h_крda/dt + Jd²a/ dt², (2-18)

где C_кр - коэффициент жесткости стержня; J - момент инерции маховика; h_к - коэффициент потерь на трение, пропорциональное скорости вращения; t - время.

Продифференцируем (2-18) по t

W₁- W₂= (1/C_кр)[dM_кр/dt+ h_крdW₂ /dt + Jd²W₂ / dt²]. (2-19)

 

Это уравнение позволяет описать колебания маховика изображенные на рис. 2.6,в.

В случае гармонического колебания частоты вращения ведущего конца, например, по закону W₁= W_1оsin(wt), (w - круговая частота) скорость вращения маховика будет изменяться следующим образом

W₂= W_2оsin(wt+j).

Это также получается из уравнения (2-18). Причем амплитуда колебаний частоты вращения маховика может быть равной W_1о , значительноменьшей, чем W_1о ( это происходит когда колебания из- за потерь не доходят до маховика), или больше, чем W_1о . Последнее возникает в случае резонанса.

Очень важным параметром, описывающим динамические свойства рассмотренной на рис. 2.6,а конструкции, является угол j. Его обычно называют сдвигом по фазе или запаздыванием по фазе. Его величина зависит от свойств материала стержня.

Вообще вопросы передачи динамической энергии через металл до сих пор полностью не ясны. Их изучением занимается реология и другие науки. В последние годы разрабатывается подход к анализу передачи энергии с учетом 4-х мерной модели упругого тела[3], где экспериментальные результаты рассматриваются под иным углом зрения. Здесь мы будем опираться на уже проверенную за много лет методику.

Эксперименты показывают, что процесс передачи колебаний по упругому стержню приводят к его нагреванию, т.е. упругая энергия частично превращается в тепловую. Существует много гипотез по этому вопросу. Рассмотрим некоторые[4].

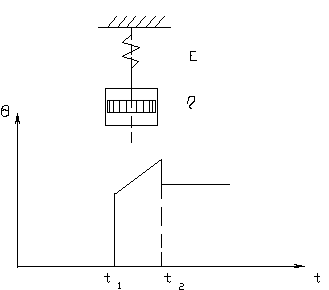
Модель Максвелла (рис.2.7)

Имеется тело, которое под действием напряжения упруго деформируется и в то же время может течь.

Общая деформация равна

q= q₁+q₂ .

После дифференцирования по времени, получим q¢ = q ¢ ₁+q ¢₂ .

При наложении напряжения, когда t=t₁, пружина мгновенно растягивается на величину s/ Е, а поршень начинает равномерно перемещаться со скоростью s/ h. В момент времени t₂ напряжение снимается, пружина мгновенно сокращается, но поршень остается в выдвинутом положении.

Реологическое дифференциальное уравнение записывается в форме

q¢ = s/h + s¢/ Е. (2-20)

Здесь q¢= dq / dt; s¢= ds / dt.

Если тело деформируется до q= q_о , а затем удерживается в этом состоянии, то q¢= 0 и

s/h + s¢/ Е= 0.

Решение его s = s_о exp(- Et/h), т.е. s экспоненциально снижается.

Величина t= h/ Е называется релаксационной постоянной.

Рис. 2.7.

Реологическая модель Максвелла.

Е- продольный модуль упругости; h- вязкость.

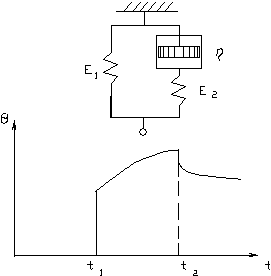
Модель Зинера (рис. 2.8)

Рис. 2.8.

Реологическая модель Зинера

Дифференциальное уравнение записывается в форме

s+ hs¢/ Е₂= Е₁q + hq¢. (2-21)

Это более общая модель. Если q¢=0, то уравнение преобразуется

s+ hs¢/ Е₂= Е₁q_о

с решением

s(t)= E₁q_o+ (s_o- E₁q_o)exp(- t/t_e), (2-22)

где t_e= h/Е₂- время релаксации при условии постоянной деформации.

Если же s¢= 0, то

q(t)= E₁s_o+ (q_o- s_o/E₁)exp( -t/t_s),

где t_s= h/ Е₁- время ретардации (запаздывания).

Тогда общее уравнение записывается в форме

s+ t_es¢ = Е₁(q+t_sq¢ ). (2-23)

Реологические исследования дали основание ввести дополнение к закону Гука, учитывающее в комплексной форме особенности передачи динамических воздействий

Е_w= s(jw)/ q(jw)= E_u + jE_v. (2-24)

Измеряя скорость распространения звуковых волн и коэффициент затухания, определяют Е_w. Кроме того, для динамического модуля упругости характерна нелинейная зависимость- гистерезисная петля, показанная на рис.2.9.

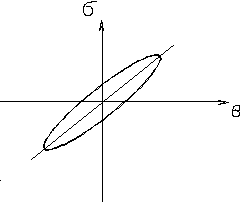
Рис.2. 9.

Гистерезисная петля.

Вообще упругость отражает способность металла деформироваться под действием нагрузки и затем возвращаться в прежнее состояние.

При растяжении (сжатии) упругая деформация металла описывается законом Гука s= Ee. Здесь e = D l/ l; Е- называют модулем упругости или модулем Юнга (для стали Е= = 2*10⁵МПа).

Если обратиться к кристаллам, то этот закон может быть выведен из рассмотрения упругого взаимодействия атомов. Взаимосвязь сил отталкивания и притяжения имеет такой же характер, как и при взаимодействии ионов и электронов в атоме рис.2.5. На больших расстояниях а притяжение и отталкивание пренебрежительно малы, но при сближении они возрастают. При таком выводе следует, что в зоне больших упругих деформаций закон Гука становится нелинейным.

В случае скручивания закон Гука записывается в форме t= GJ- для малых деформаций. Здесь t- максимальное касательное (скалывающее) напряжение; G- модуль сдвига (для стали G= 8*10⁴МПа); J- угол сдвига (поворота) в радианах. Полный поворот сечения на расстоянии z от начала координат равен j=J‘z, где J‘= dj/ dz- относительный угол закручивания. Для вала J‘=М_к /(GJ_p). Здесь J_p- полярный момент инерции сечения; М_к - крутящий момент.

Модули упругости определяют статическими и динамическими методами.

Статические. Под действием нагрузки происходит растяжение. Измеряя последнее , определяют модуль упругости E.

Недостаток- Чтобы получить точный результат нужна большая деформация, но при этом есть вероятность пластической деформации.

Динамические. Модуль сдвига G определяют по частоте крутильных колебаний. Модуль упругости E определяют по частоте изгибных колебаний.

Импульсный метод основан на определении скорости распространения волн через образец.

При удлинении образца происходит одновременно его сужение. Это оценивается коэффициентом Пуассона

m= (Dd/d)/(Dl/l).

Модули продольной упругости Е и сдвига G связаны соотношением

G= 0,5E(1+m).

При всестороннем сжатии

s= KDV/ V,

где К- модуль всесторонней объемной упругости; DV - изменение объема.

Приближенно DV/ V @ 3 Dl/ l= 3s / E, т.е. s/К= 3s/Е. Откуда К= Е/ 3.

§2.4. Общие свойства металлов и сплавов, как веществ,