Основные металлические свойства металлов.
1. Высокая тепло и электропроводность.
Носителями тока в металлах являются электроны проводимости, т.е электронный газ. Упорядоченное движение электронов в металлическом проводнике возникает под действием внешнего электрического поля. Плотность тока равна
`j = no e `v , (2- 1)
где no- число электронов проводимости в единице объема; e- абсолютная величина заряда электрона; `v- средняя скорость упорядоченного движения электронов. При наибольших допустимых плотностях токов v= 10-2 см/ сек. Время установления тока в цепи равно t= L/c, где L- длина цепи; с- скорость света в вакууме.
Теплопроводность в металлах обусловлена, в основном, передачей энергии электронами проводимости, однако, частично, она осуществляется колебаниями атомов в кристаллической решетке.
2. Электропроводность. Положительный температурный коэффициент электросопротивления.
Закон Ома для плотности тока записывается в форме
j= E/ rэ, (2-2)
где Е- напряженность электрического поля; rэ- удельное сопротивление.
Для всех металлов произведение коэффициента теплопроводности К на удельное сопротивление пропорционально абсолютной температуре Т иравно
Кrэ= 3(k/e)2Т , (2-3)
где k- постоянная Больцмана.
Удельное сопротивление проводника зависит от температуры следующим образом
rэ= rо(1+ at), (2-4)
где rо - удельное сопротивление при 0°С; a- температурный коэффициент сопротивления; t- температура в градусах Цельсия.
Для большинства металлов в интервале температур 0- 100°С коэффициент a меняется в пределах (3,3- 6,2)10-4град-1.
В некоторых металлах и сплавах наблюдается сверхпроводимость, когда при определенной температуре (Al- T°K=1,2; Nb3Sn- TT°K=18...), ниже критической, электрическое сопротивление становится исчезающее малым.
Сверхпроводимость проводника исчезает при пропуске достаточно сильного тока.
Теория сверхпроводимости рассматривает это явление, как сверхтекучесть электронов в металле. Особое взаимодействие между электронами может привести к их взаимному притяжению (образованию связанных пар). Этот эффект может в ряде случаев стать причиной перехода в сверхпроводящее состояние. В системе таким образом связанных электронов в атоме образуется единый коллектив электронов, который не может отдавать энергию частями, т.е. энергия электронов не тратится на тепловые колебания ионов.
Для постоянного тока i связь с напряжением U и сопротивлением R описывается уравнением Ома
R= U/ i. (2-5)
Причем R= rэ l/s, где rэ = rэо(1+ at); ro - удельное сопротивление при 0°С; a- температурный коэффициент.
В таблице 2.1 приведены некоторые характеристики металлов.
Табл. 2.1
| Обозначе-ние вещества | Удельное сопротивление, rэ ,Ом*мм2/м | Температурный коэффициент, град-1 | Примечание |
| Al | 0,028 | 0,0049 | Наиболее часто применяют в качестве проводников |
| Cu | 0,0175 | 0,0039 | |
| Fe | 0,098 | 0,0062 |
(Диэлектрики имеют высокое rэ и их используют для электроизоляции. Полупроводники применяют при изготовлении выпрямителей и других радиотехнических устройств.)
В случае переменного тока сопротивление R зависит также от частоты колебаний f, от индуктивности L и емкости С. На рис. 2.2 показано изменение сопротивления проводника, представляющего собой последовательный резонансный контур, от частоты переменного тока при активном сопротивлении Ra= 100 Ом и разных значениях индуктивного и емкостного сопротивлений[2].

|
| Рис. 2.2 Изменение сопротивления прводника: L- индуктивное, С- емкостное, пунктир- общее сопротивление. |
Если имеет место параллельный резонансный контур, то характер изменения сопротивления будет иной.
В случае воздействия на металлический проводник переменного тока высокой частоты из-за явления самоиндукции плотность тока будет максимальной в поверхностном слое. Глубина его проникновения оценивается по выражению
x=503,3[rэ/(mf), (2-6)
где m - магнитная проницаемость.
Чем выше частота колебаний f , тем меньше x. Это явление называют скин-эффектом. На его действии во многом основана закалка ТВЧ (токами высокой частоты).
3. Теплопроводность.
Обычно обозначается символом l, который равен количеству тепла, переносимому через единицу поверхности за единицу времени при градиенте температуры, равном единице.
dQ=- ldsdt(dT/dx) . (2-7)
В металлах теплопроводность состоит в передаче тепла из нагретой точки в более холодную. Этот процесс описывается уравнением
¶T/¶ t=aDT+ qv / (cr), (2-8)
где a= l/ (cr)- коэффициент температуропропроводимости. Он характеризует скорость выравнивания температур; с - удельная теплоемкость.
Пример:
Al- l= 209,3 вт/(м*град);
Fe - 74,4 -”-;
Cu - 389,6 -”-.
4. Термоэлектронная эмиссия.
Это испускание электронов нагретыми металлами. Термоэлектронная эмиссия становится интенсивной при температуре металла несколько сотен градусов по Кельвину.
5. Металлы непрозрачны и имеют металлический блеск.
6. Повышенная способность к пластической деформации.
При изменении температуры изменяются размеры металлической детали. Это описывается уравнениями
l= lo(1+alDt), V=Vo(1+aVDt), (2-9)
где lo, Vo - первоначальные длина и объем тела; al, aV - коэффициенты линейного и объемного расширения.
Заметим, что aV= 3al .
7. Коррозионная стойкость (см. также § 2.19).
Коррозия - разрушение металлов и сплавов под действием окружающей Среды. Металлы обычно ржавеют. Из-за этого резко ухудшаются механические свойства, иногда при отсутствии изменения внешнего вида поверхности.
Есть химическая коррозия- от воздействия газов, нефти и ее производных, и электрохимическая коррозия- от кислот, щелочей и солей (электролиты).
Электрохимическая коррозия. Если в электролит (водные растворы кислот, солей, влажный воздух) поместить 2 соприкасающихся различных металла, то образуется гальванический элемент. Металл легче отдающий электроны- анод, а другой- катод. В процессе работы гальванического элемента анод разрушается.
8. Магнитные свойства металлов.
Электрон обладает собственным моментом количества движения (вращение относительно своей оси) - спином. Это механический момент ps= ± h/ (qp). Он имеет только 2 ориентации относительно внешнего магнитного поля, направленного по оси. Спину ps соответствует спиновой магнитный момент pms= qsps (qs - гиромагнитное отношение).
Спином электрона объясняется структура спектральных линий, распределение электронов по энергетическим состояниям в атомных системах, магнитные свойства ферромагнетиков.
Однородное магнитное поле, куда внесен атом, изменяет угловую скорость вращения электронов. При этом они вокруг ядра вращаются по разным направлениям.
По магнитным свойствам металлы делятся на диамагнитные (а), парамагнитные (б), ферромагнитные (в):
а- Это вещества (Zn, Au, Hg...), где индуцирование дополнительного отрицательного магнитного момента в атомных электронных оболочках происходит под действием внешнего магнитного поля. При этом суммарный магнитный момент в теле уменьшается. Один из диамагнетиков- сверхпроводник. У него внутренний магнитный поток равен нулю.
б- Это вещества (Li, Na, K...), у которых при отсутствии внешнего магнитного поля собственный сумарный магнитный поток из- за теплового движения атомов равен нулю.
При внесении парамагнетика в магнитное поле происходит переориентация всех атомов по направлению поля. После вынесения В=0.
Если магнитные материалы легко намагничиваются при приложении электрмагнитного поля и размагничиваются при снятии, то они называются магнитомягкими.
в- Вещества (Fe, Ni, Co...), собственное магнитное поле которых может в тысячи раз превышать внешнее.
Имеет место также и антиферромагнетизм, когда ориентация спиновых магнитных моментов становится противоположной. В одном кристалле может возникнуть явление ферромагнетизма и антиферромагнетизма. Если массивы таких элементов одинаковы, то намагничивания кристаллов не будет. Особые свойства ферро- и антиферромагнетиков обнаруживаются при температурах, называемых точками Кюри (qк). При Т<qк тело разбито на домены - малые области самопроизвольной намагниченности. Ферромагнитные матералы обладают доменной структурой. Если напряженность магнитного поля H =0, то направления векторов намагниченности разных доменов не совпадают. В итоге суммарная намагниченность равна нулю, но после приложения вектора Н многие векторы направляются параллельно Н.
Монокристаллы ферромагнетиков могут сильно намагничиваться в одном направлении.
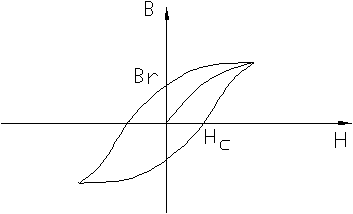
|
Рис. 2.3
Магнитная гистерезисная петля.
Вr - остаточная индукция;
Нс - коэрцитивная сила.
Для ферромагнетиков имеет место магнитный гистерезис, отставание изменения магнитной индукции В от изменения напряженности Н (см. рис. 2.3). Чем меньше Нс, тем легче перемагничивается материал. Такие материалы называются магнитомягкими.
Это следствие необратимых изменений при намагничивании и перемагничивании.
Магнитострикция- изменение формы и размеров ферромагнетика при его перемагничивании. Здесь под действием Н домены разворачиваются, приводя к изменению формы и размера. Возможно также изменение намагниченности из-за деформации.
9. Твердость.
Твердость металлов и сплавов обычно оценивается 3-мя методами (см. рис. 2.4):
а) методом Бринелля- по вдавливанию стального шарика в деталь (HB).
б) методов Роквелла- по вдавливанию алмазного конусного наконечника или стального шарика Æ 1,588 мм в деталь (HRCэ) (см. также стр.24).
в) методом Виккерса- по вдавливанию 4-х гранной алмазной пирамидки (HV).
По методу Бринелля используют шарики диаметром 10 мм и 5 мм. В 1-м случае вдавливают шарики силой F= 29740 Н (3000 кГс), а твердость, обозначаемую HB, определяют по диаметру do отпечатка ГОСТ:
HB=2F0,102/[pd(d- (d2 -d2o)0,5],МПа. (2-10)
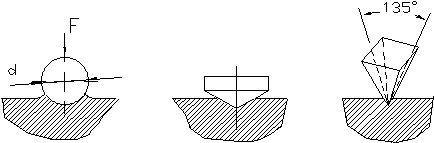
|
Рис. 2.4 Способы определения твердости.
по Бринеллю по Роквеллу по Виккерсу
Оценим давление, развивающееся под шариком:
p= 4F/(p d 2o)
Получим при do= 5,6мм p= 1192,7 МПа. В то же время для такого материала предел текучести составляет 300 МПа. Это означает, что металл течет и образует наплыв. Вещество, находящееся в пластическом состоянии, дросселирует через щель, образованную стенкой шарика и недеформированными участками поверхности детали. Чем выше прочность материала, тем меньше отмеченная щель и тем меньше диаметр отпечатка. По нашим исследованиям для шарика диаметром 10 мм давление в материале можно оценить формулой
p= 4,64F0,094HB0,99 , МПа. (2-11)
Здесь F подставляется в Н.
Тогда диаметр отпечатка для стали равен
do= 0,524F0,453/HB0,495. мм (2-12)
Метод Бринелля применяется для металлов имеющих твердость до 450 единиц, поскольку шарик может деформироваться.
При определении твердости по Роквеллу алмазный конус используется для твердых металлов, шарик- для мягких.
Конус и шарик вдавливают 2-мя последовательными нагружениями Ро = 10 кГс (98 Н) и основной Р1= 90 кГс (882 Н) для шарика (шкала В®HRB) и конуса 140 кГс (1372 Н) - шкала С® (HRC). При испытании очень твердых и более тонких материалов используется алмазный наконечник (шкала А HRA при усилии 50 кГс, 490 Н). Твердость по Роквеллу измеряют в условных единицах. Единица- осевое перемещение наконечника на 0,002 мм.
Обозначение HRCэ- это твердость, воспроизводимая государственным эталоном.
Испытания по Виккерсу применяют для определения твердости деталей малой толщины и тонких поверхностных пленок, имеющих высокую твердость.
Твердость в этом случае имеет следующее обозначение
HV= 1,8544P/d2, (2-13)
d- средне-арифметическое 2-х диагоналей отпечатка.
В таблице 2.2 приведено соответствие твердости, определенной разными методами
Табл. 2.2
| HB | HRA | HRC | HRB | HV | HB | HRA | HRC | HRB | HV |
| - | - | - | 34,8 | - | |||||
| - | - | - | 36,7 | - | |||||
| - | - | - | 35,6 | - | |||||
| - | 40,6 | - | |||||||
| - | 42,5 | - | |||||||
| - | - | ||||||||
| - | 73,5 | 47,5 | - | ||||||
| 23,1 | 50,3 | - | |||||||
| 26,5 | - | 53,2 | - | ||||||
| 28,9 | - | 78,5 | 55,1 | - | |||||
| 31,8 | - | 79,5 | 57,6 | - | |||||
| - |
Микротвердость определяется в тонких листа, фольге, пленках, в отдельных точках деталей при толщине не меньшей 10 кратной глубины отпечатка. Используют алмазные наконечники в форме 4-х гранной пирамиды (условное обозначение H–) для более мягких и толстых материалов, 3-х гранной пирамиды (HÑ), ромбической пирамиды, бицилиндра. В процессе измерения используют гири массой 5; 10; 20; 50;...500 г. Результаты определяются по таблицам.
Микротвердость может измеряться царапанием поверхностного слоя 4-х гранной или 3-х гранной пирамидками под действием нормальной нагрузки Р= 0,005- 0,2 кГс. Выражается она числами от деления Р на условную площадь контакта пирамиды с испытуемой поверхностью.
Пластичная твердость (HD)определяется вдавливанием сферического наконечника диаметром D в испытуемую поверхность с последовательными нагрузками Р и Р1 . Тогда
HD= (P- P1)/[pD(h-h1)] . (2-14)
Динамическая твердостьоценивается специальным прибором по высоте отскакивания ударного бойка или времени затухания колебаний маятника. Современные приборы снабжены электроникой и позволяют определить твердость в любом положении. Это преимущество перед традиционным определением HB.
Дата добавления: 2015-02-19; просмотров: 837;
