Упругость насыщенных паров над раствором
В отличие от газов и жидкостей, конвекция в твердых телах невозможна, поэтому единственным механизмом переноса тепла в твердом теле является теплопроводность. Процесс переноса тепла фактически является процессом распространения тепловых колебаний в решетке, то есть распространения со скоростью звука волн, которые и переносят энергию колебаний. Как и в жидкостях и газах, перенос тепла в твердом теле описывается уравнением теплопроводности (7.15). Приближенная теоретическая формула для коэффициента теплопроводности твердого тела выводится на основе квантовых представлений. При этом распространяющимся в теле со скоростью звука колебаниям сопоставляются фиктивные частицы - фононы. Каждый фонон обладает энергией, которую и переносит от одной части тела к другой.
В металлах, наряду с колебаниями решетки, перенос тепла осуществляют и свободные электроны, причем в широком интервале температур перенос тепла электронами во много раз больше, чем фононами. Этим объясняется высокая теплопроводность металлов по сравнению с непроводящими телами, в которых фононный (решеточный) механизм теплопроводности является практически единственным. Например, при нормальной температуре коэффициент теплопроводности алюминия равен  , тогда как у кварца он равен
, тогда как у кварца он равен 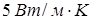 . Для сравнения заметим, что у газов при нормальных условиях коэффициент теплопроводности по порядку величины равен
. Для сравнения заметим, что у газов при нормальных условиях коэффициент теплопроводности по порядку величины равен 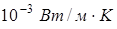 .
.
Так же, как и в газах, атомы в твердом теле имеют различные энергии теплового движения. При любой температуре имеется некоторая часть атомов, энергия которых достаточно велика для того, чтобы эти атомы могли покинуть свои узлы и занять новые положения. С ростом температуры число таких атомов возрастает, соответственно, возрастает коэффициент диффузии в твердом теле. По величине он на много порядков меньше, чем у жидкостей и тем более у газов.
Упругость насыщенных паров над раствором
Рассмотрим бинарный раствор, состоящий из двух веществ: растворителя 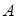 и растворенного вещества
и растворенного вещества 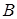 . В насыщенном паре над раствором содержатся как молекулы вещества
. В насыщенном паре над раствором содержатся как молекулы вещества 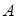 , так и молекулы вещества
, так и молекулы вещества 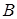 . Соответственно, можно говорить о парциальных давлениях
. Соответственно, можно говорить о парциальных давлениях 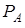 и
и 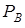 этих веществ в насыщенном паре над раствором. Следует ожидать, что эти давления пропорциональны относительным количествам молекул веществ
этих веществ в насыщенном паре над раствором. Следует ожидать, что эти давления пропорциональны относительным количествам молекул веществ 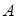 и
и 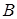 в растворе:
в растворе:
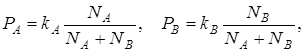 (13.2)
(13.2)
где 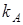 ,
, 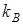 - коэффициенты пропорциональности,
- коэффициенты пропорциональности, 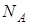 и
и 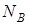 - числа молекул веществ
- числа молекул веществ 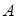 и
и 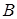 в растворе. При
в растворе. При 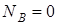 должно быть
должно быть 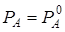 , где
, где 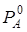 - давление насыщенного пара чистого вещества
- давление насыщенного пара чистого вещества 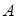 . Отсюда заключаем, что
. Отсюда заключаем, что 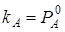 . Аналогично находим, что
. Аналогично находим, что 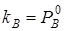 , где
, где 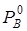 - давление насыщенного пара чистого вещества
- давление насыщенного пара чистого вещества 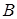 . Полагая в (13.2)
. Полагая в (13.2) 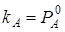 ,
, 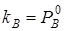 и поделив числители и знаменатели дробей на число Авогадро, получим:
и поделив числители и знаменатели дробей на число Авогадро, получим:
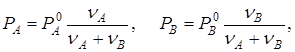 (13.3)
(13.3)
где 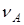 ,
, 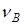 - количества молей веществ
- количества молей веществ 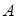 и
и 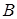 в растворе. Равенства (13.3) выражают закон Рауля. Этот закон достаточно хорошо выполняется для растворов, близких к идеальным.
в растворе. Равенства (13.3) выражают закон Рауля. Этот закон достаточно хорошо выполняется для растворов, близких к идеальным.
Пример 13.2. Давление насыщенного пара над раствором, состоящим из веществ 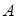 и
и 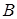 , равно
, равно 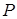 . При той же температуре давления насыщенных паров чистых веществ равны
. При той же температуре давления насыщенных паров чистых веществ равны 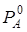 и
и 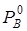 . Найдем отношение
. Найдем отношение 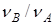 числа молей вещества
числа молей вещества 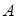 к числу молей вещества
к числу молей вещества 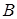 .
.
Воспользуемся законом Рауля (13.3). Складывая парциальные давления 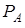 и
и 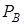 и учитывая, что
и учитывая, что 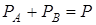 , получим:
, получим:
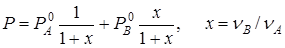 .
.
Получившееся уравнение имеет при  решение вида:
решение вида:
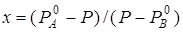 .
.
Дата добавления: 2015-02-05; просмотров: 1123;
