Степень полимеризации

Проводя статистический анализ полимерных молекул, приходится определять, сколько содержится в образце молекул каждого сорта, или каково среднее число мономерных звеньев в полимерной молекуле, какова вероятность общей заданной конформации, каково среднее расстояние от одного конца молекулы до другого и тому подобные задачи. Этому и посвящен данный раздел. С точки зрения биофизики (и молекулярной биологии) ответы на эти вопросы будут во многом способствовать выяснению физико-химических свойств биомакромолекул и, в конечном итоге, особенностей их функционирования.

Степенью полимеризации полимерной молекулы называется число структурных субъединиц, содержащихся в молекуле – х. Молекула со степенью полимеризации х называется х-мером. Определение годится и для разветвленных полимеров. В простом линейном полимере идентичны все звенья, кроме концевых.

Молекулярная масса М_х х-мера является суммой молекулярных масс всех х звеньев. При больших х (х>100) концевыми эффектами можно пренебречь и считать, что все звенья имеют молекулярную массу М_о, тогда:

М_х = хМ_о,

где М_о – константа для полимера данного типа (не зависит от х), поэтому термины молекулярная масса и степень полимеризации в какой-то степени идентичны.

Распределение по молекулярным массам

Степень полимеризации полимеров даже одного типа (как искусственных, так и природных) может колебаться в широких пределах. Распределение по молекулярным массам описывает частоту нахождения данной степени полимеризации. Наиболее обычным является задание изменения мольной доли х-мера (Х_х) как функции х, т.е. Х_х = f(х)

Подобное уравнение называется функцией распределения. Х_х – доля от общего числа молекул, приходящихся на х-мер.

Например, функция распределения для поликонденсации, при которой не изменяется реакционная способность функциональных групп в зависимости от х:

OH-R-COOH 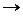H-[-O-R-CO-]_x-OH + H₂O

Пусть в начальном состоянии N_о мономеров, т.е. по N_o функциональных групп каждого типа. Пусть полимеризация протекает до тех пор, пока не прореагирует доля р от всех функциональных групп. Число оставшихся функциональных групп каждого типа равно тогда N_o(1-p). Но это же число определяет и число независимых молекул, так как каждая молекула имеет концевые не прореагировавшие группы.

Среднечисловая степень полимеризации 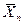определяется как среднее число мономерных звеньев в молекуле и равна:

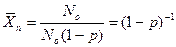
Для того, чтобы 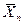было >100, значения р должны лежать между 0,99 и 1,00, так как говорим о макромолекулах.

Предположим, что все молекулы в конечной смеси расположены друг за другом вдоль конечного отрезка. Пусть он состоит из N_o звеньев структуры. В р•N_o местах звенья будут соединены СО-О-связями, в остальных (1-р)N_o местах связей нет. В нашем конечном отрезке будут точки, где кончается одна молекула и начинается другая. Если реакционная способность функциональных групп не зависит от длины цепи, размещение этих точек будет случайным.

Вычислим вероятность того, что данная структурная единица (звено) является частью х-мера. Чтобы вычислить эту вероятность, нужно сначала определить вероятность того, что выбранное звено является начальной частью х-мера. Эта вероятность равна вероятности того, что вдоль нашего отрезка расположатся (х+1) состояний в последовательности:

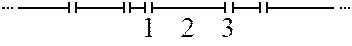
1 – несвязанное состояние; 2 – (х-1) СО-О-связей; 3 – следующее несвязанное состояние. Остальные состояния могут быть либо связями, либо промежутками.

Так как эти состояния являются независимыми, вероятность того, что мы имеем в данном месте начинающийся х-мер, является произведением вероятностей нужного нам события для каждого состояния. Эта вероятность равна р для имеющих связи и (1-р) для не имеющих связи состояний (так как доля связанных функциональных групп – это и есть мера вероятности того, что в данном состоянии есть связь). 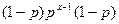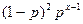Таким образом, вероятность того, что выбранное звено является начальной частью х-мера, равна или (х-1, так как х звеньев связаны х-1 связью).

Для всех других, кроме интересующих нас (х+1) состояний вероятность равна 1, так как не имеет значения, связаны они или нет. (х+1) здесь, так как одно несвязанное состояние плюс (х-1)-связей плюс второе несвязанное состояние с другого конца х-мера. Но нам надо определить вероятность того, что данное звено является частью x-мера. Если это звено должно быть частью любого х-мера, то вдоль цепи имеется х состояний, с которых можно начать отсчет. Таким образом, полная вероятность того, что выбранное звено является частью х-мера, равна 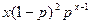. Так как молекула может состоять из одного звена, то эта же вероятность может быть и вероятностью того, что этот х-мер является долей от общего числа х-меров.

Вероятность того, что данная структурная единица (звено) входит в х-мер, эквивалентна доле структурных единиц, составляющих х-меры. Считая, что все звенья имеют одинаковую массу, эта вероятность эквивалентна также весовой доле х-мера W_x:

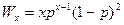(надо учитывать выделение воды при поликонденсации).

Это и есть распределение по массам (называют чаще весовым распределением). Оно показывает долю от общей массы, приходящуюся на х-мер.

Определим теперь числовое распределение, т.е. долю от общего числа молекул, приходящуюся на х-мер. Общая масса равна N_oM_o/N_A, где М_о – молекулярная масса структурной единицы –СО-R-О-, N_A – число Авогадро. Масса всех молекул х-мера равна W_xN_oM_o/N_A. Масса каждой х-мерной молекулы равна хM_o/N_A и число х-мерных молекул равно W_xN_o/х. Мы отметили, что общее число всех молекул равно N_o(1-p), поэтому мольная доля х-мера может быть записана так:

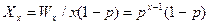
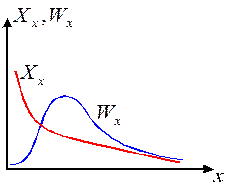
Рис.10 Зависимость весового и числового распределения от числа звеньев

Это и есть числовое распределение, т.е. доля от общего числа молекул, приходящаяся на х-мер (или мольная доля).

Комбинируя полученные выражения для распределений с выражением для 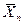, можно отметить, что W_x>X_x, когда х> 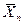и W_x<X_x, когда х< .

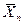Сумма всех весовых (W_x) долей и всех мольных (X_x) долей равна единице.

;

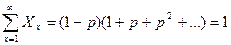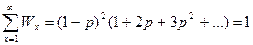
Функции на этих рисунках не непрерывны (х – целочисленные), но при больших х можно эти разрывные функции заменить непрерывной функцией распределения:

; ,

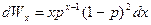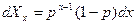где 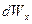- бесконечно малая доля веса полимера, имеющего степень полимеризации между х и х+dх. Преимущество функций такого рода в том, что х можно интегрировать в конечных пределах.

Приведенные распределения – это частный случай распределений, которые могут быть получены при синтезе полимеров. Тип распределения зависит от кинетики полимеризации.

Фракционирование полимеров

Фракционирование гетерогенных полимеров производят:

- используя их различия в растворимости, связанные с разными длинами цепи;

- с помощью ультрафильтрования через градуированные мембраны;

- с помощью хроматографии на колонках;

- с помощью ультрацентрифугирования.

В результате получают более гомогенные растворы полимеров, с более узким распределением.