Энергия взаимодействия звеньев.

Изменение температуры приводит к изменению размеров макромолекулы, т.е. к изменению средней плотности n числа мономерных звеньев, а значит, и к изменению энергии их взаимодействия. Вклад сил притяжения и отталкивания в свободную энергию взаимодействия (F) звеньев зависит от n. При малом n свободная энергия (F) взаимодействия звеньев может быть разложена в ряд со степенями n:

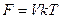(Bn²+Cn³+…),

где V – объем системы, В и С – коэффициенты разложения, называемые вириальными коэффициентами (В – второй вириальный коэффициент; С – третий и т.д.).

Первое слагаемое ~Вn² – описывает вклад парных столкновений звеньев, второе – вклад тройных столкновений и т.д. Если энергия притяжения при столкновениях велика по сравнению с kT, то силы притяжения сталкивающихся частиц играют наиболее важную роль, давая отрицательный вклад в общую энергию системы (В<0). В результате макромолекула сжимается относительно размеров идеального клубка. Обратная картина, когда энергия притяжения меньше kT, а силы отталкивания дают в свободную энергию положительный вклад, вызывая набухание клубка (B>0). В отсутствие объемных взаимодействий при q-температуре В(q)=0.

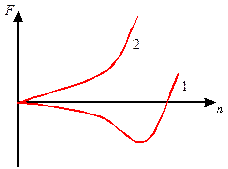
Случаю плохого растворителя отвечает B<0. Случаю хорошего растворителя отвечает B>0 (звенья отталкиваются). Типичный вид зависимости F глобулы от n: зависимость свободной энергии глобулы (1) и клубка (2) от плотности звеньев.

Рис.8 Типичный вид зависимости свободной энергии макромолекулы от плотности звеньев. 1 – глобула 2 – клубок

Кривая 1 (Рис.8) соответствует B<0 и С>0, т.е. третий вириальный коэффициент положительный. Таким образом, в простейшем случае, когда B<0, вклад отталкивания (С>0) доминирует уже при столкновениях трех частиц. При изменении температуры и других условий в растворе вириальные коэффициенты изменяются и, следовательно, меняется величина F.

Переходы клубок-глобула

Когда F перестает иметь минимум при некотором n глобула распадается и происходит переход глобула-клубок (Г-К). Точке перехода соответствует F=0. Это переход между разными фазами (между разными агрегатными состояниями макромолекулы).

Фазовые переходы I рода происходят между двумя состояниями, каждое из которых стабильно по одну сторону от точки перехода и метастабильно – по другую. Переход между ними при изменении внешнего параметра (Т) сопровождается тепловым эффектом (например, плавление льда и образование жидкой водной фазы).

Фазовые переходы II рода происходят без тепловых эффектов, а в области перехода существует лишь один минимум свободной энергии.

При фазовых переходах I рода энтропия и внутренняя энергия меняются скачком вследствие затраты конечной теплоты перехода и конечного изменения удельного объема системы.

При фазовых переходах II рода в точке перехода 2-го рода теплоемкость меняется скачком, а энтропия и внутренняя энергия – непрерывно, удельный объем системы не испытывает скачка. (Переход Не в сверхтекучее состояние, металлов в сверхпроводящее, переход из ферромагнитного в парамагнитное состояние в точке Кюри).

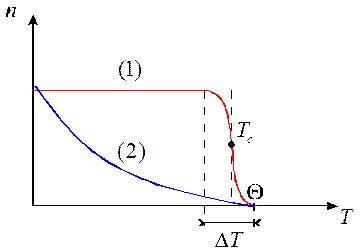
Фазовые переходы определены строго для случая, когда число частиц в системе N®¥. В реальных полимерах, где N – большое, но конечное число, существует конечная ширина температурного перехода (DТ). Конформационный переход является фазовым, если его ширина стремится к 0: DT>0 при N®¥. Ландау иЛившицем, Гросбергом и Хохловым было показано, что в случае жесткой цепи переход клубок - глобула происходит как фазовый переход I рода (1), хотя и с малой теплотой перехода. Для гибких молекул переход происходит как фазовый переход II рода (2).

Рис.9 Фазовые переходы для жестких (1) и гибких (2) макромолекул

Конечный скачок плотности наблюдается несколько ниже q-точки, причем 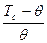~ 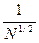. В случае гибких цепей переход происходит как плавный переход II рода, растянутый на всю q-область.