Персистентная длина

Отклонение от гауссовой статистики могут наступать при небольшом числе (меньше 20-50) связей в полимерной цепи и молекулярных массах в несколько сотен единиц. Однако известны полимеры (ДНК в форме двойной спирали, спиральные полипептиды), в которых даже при 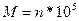цепь не подчиняется гауссовой статистике, а длина сегмента цепи существенно увеличивается. 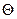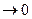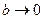Такие жесткие молекулы моделируются червеобразной цепью, у которой в пределе среднее значение угла между звеньями при , а цепь имеет непрерывную структуру (кривизну еще надо показать, т.к. бывает отрицательная).

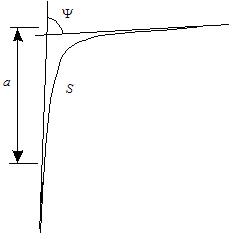Рис.6 Участок жесткой макромолекулы

а - персистентная длина, S – контурная длина, 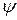- угол между касательными к двум участкам цепи, разделенным достаточно большой длиной S.

Среднее значение cos 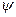между касательными к двум участкам цепи, разделенным достаточно большой длиной S вдоль нити, убывает экспоненциально с ростом S:

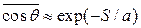, где а –

персистентная длина.

Из этой формулы видно, что 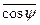при S=a уменьшается в e раз. Короткий по сравнению с a участок цепи ведет себя как твердый стержень, а разные сегменты длиной a вращаются практически независимо друг от друга. Для червеобразной цепи среднеквадратичное расстояние связано с ее персистентной длиной: 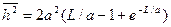, где L-контурная длина цепи. При бесконечно жесткой цепи (жесткий стержень) 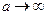, т.е. 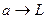, и 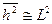. Напротив, в случае гибкого стержня 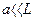образуется обычный гауссовый клубок, где .

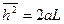Для молекулы ДНК, представляющей собой жесткий полимер, персистентная длина составляет 50-60 нм, что намного больше, чем у большинства обычных гибких полимерных молекул. Жесткость ДНК определяется взаимодействием оснований, расположенных стопкой вдоль спирали и соединенных сахарофосфатными связями.