Поворотно-изомерная теория макромолекул

Свободно-сочленённая цепь

Рис.5

В цепи полиэтилена, который состоит из единичных связей С—С, внутренние повороты происходят в каждом звене цепи. Именно внутренним вращением и определяется гибкость цепи, ответственная за высокоэластичность полимера. Предположим, что цепь свободно сочленена, т.е. в ней нет фиксированных валентных углов, и повороты происходят свободно. Набор конформаций, возникающих при поворотах вокруг данного атома цепи непрерывны в интервале углов от 0 до 4 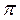и энергия при поворотах не меняется. Цепь можно охарактеризовать вектором 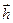, проведенным от первого атома к последнему. Очевидно, что среднее по всем конформациям значение вектора 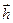равно 0. т.к. при тепловом движении его направления равновероятны. 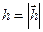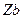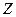Распределение вероятности осуществления тех или иных значений , которые могут меняться от 0 до максимальной длины цепи (равна , где -число звеньев, 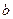-длина звена), оказывается гауссовым – вероятность того, что расстояние между концами цепи лежит в интервале от 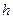до 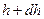имеет вид:

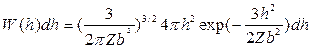
Общее Гауссово распределение имеет вид .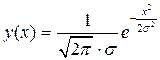

В нашем случае 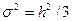. Длина вектора 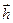равна: 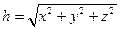, где x,y,z – проекции вектора 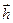на оси координат. Функции распределения координат x,y,z конца цепи являются гауссовыми и имеют вид: 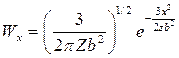и т.д.

Соответственно 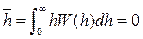и 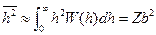т.е. цепь сильно скручена. Написанное верно при Z >>1. Тепловое движение свёртывает макромолекулу в клубок. Это состояние наиболее вероятно, т.к. клубкообразная конформация может реализовываться множеством способов (тогда, как вытянутая – только единственным способом). Поэтому клубкам соответствует максимальная энтропия:

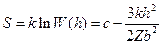, где .

Упругая сила при растяжении цепи равна: 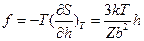, т.е. модуль упругости линейно зависит от Т ( )

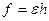В реальных макромолекулах валентные углы между связями фиксированы и повороты не свободны. Зададим положение двух первых звеньев в полиэтиленовой цепи. Третье звено может занимать различные положение на поверхности конуса с раствором 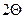( 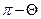- это валентный угол между связями С—С, близкий к тетраэдрическому ).

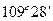Этим различным положениям, характеризуемым углом поворота 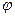вокруг второй связи С—С, отвечают разные энергии 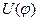. Положение четвертой связи по отношению к первым двум менее определено, так как она ориентирована на конусе, описанном вокруг каждого из положений третьей связи и т.д. Достаточно удаленная связь (звено) располагается по отношению к первой связи практически произвольным образом. Поэтому длинная цепь свертывается в клубок. Макромолекулу можно разбить на сегменты, положения которых коррелированны друг с другом. Тогда написанные формулы сохраняются, но 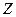и 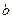означают число и длину свободно сочлененных сегментов ( 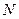и 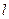). 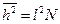при свободном сочленении.

Для реальной цепи с симметричными радикалами типа полиэтилена (но не полисахаридов). Ока получил

,

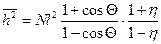где 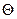- угол дополнительный к валентному, 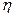- средний косинус внутреннего вращения :

,

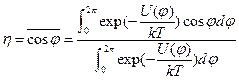где 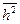- здесь больше, чем в свободно сочлененной цепи, т. к. корреляция, определяемая отсутствием свободы вращения и валентными углами, удлиняет цепь. 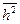может рассматриваться как мера термодинамической гибкости цепи – чем меньше 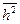при заданных 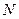и 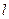, тем больше гибкость. Для жесткой цепи (транс- конформаци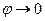и) и 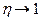, тогда

.

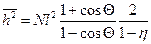Для гибких цепей это требует знания потенциальных энергий .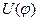

Теория размеров, формы, а также дипольных моментов, анизотропной поляризуемости и т.д. полимерных цепей должна исходить из физического механизма гибкости. Гибкость определяется поворотами вокруг единичных связей.

Поворотно-изомерная теория рассматривает макромолекулу как равновесную смесь поворотных изомеров, а внутреннее вращение в цепи – как поворотную изомеризацию (перескок из одной конформации в другую). Непрерывная функция 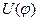заменяется в ПИТ разрывной функцией, содержащей ряд бесконечно узких щелей при фиксированных значениях 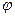. В действительности флуктуации — крутильные колебания около значений 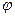, отвечающих поворотным изомерам. Но они случайны и в среднем компенсируют друг друга и не влияют на усредненные свойства макромолекулы, т. е. их можно не учитывать. В поворотно-изомерной теории (ПИТ) интегрирование для 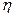заменяется суммированием по ротамерам. Так для полиэтилена: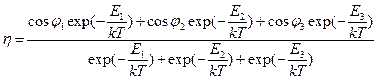

.

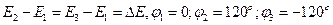
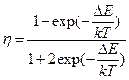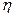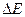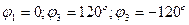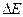
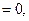
Термодинамическая гибкость макромолекулы (степень скученности статклубка), тем больше, чем меньше , т. е. чем меньше . Если минимумы энергии расположены симметрично ( ), то при 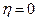макромолекула ведет себя как цепь со свободным внутренним вращением. ПИТ хороша, когда минимумы энергии разделены энергетическими барьерами больше kТ. ПИТ установлена рядом методов ИКС, доказана при деформации полимеров и легла в основу статфизики макромолекул.

Термодинамические условия кристаллизации и плавления полимеров непосредственно связаны с поворотной изомеризацией. Температура плавления Т_пл выражается как отношение разности энтальпий к разности энтропий в твердом и жидком состояниях. Увеличение энтропии при плавлении полимера связано с переходом от упорядоченной конформации цепи к смеси поворотных изомеров, к статклубку.

Кристаллическое строение характерно для волокон полимеров. Макромолекулы в волокне уложены регулярно, их цепи параллельны оси волокна (шерсть, шелк, целлюлозное волокно, белки).

Рентгеноструктурные данные Натта и Коррадини показали, что в кристалле повторяющиеся структурные единицы цепи занимают геометрически эквивалентные положения относительно её оси. Это лежит в основе постулата эквивалентности геометрических положений структурных единиц. Этот постулат дает установить симметрию цепи в кристалле и конформации мономерных звеньев исходя из стереохимического строения ее цепи и конформации. Вследствие регулярности цепи и эквивалентности звеньев молекулы полиамидов и полипептидов могут кристаллизоваться лишь в виде спиралей. Так как строение их мономеров не симметрично, спираль может быть право- и левовинтовой, оптически активной. Однако образец синтетического полимера из симметричных мономеров оптически неактивен (содержит одинаковое число левых и правых спиралей — их рацемическую смесь).

Фиксация определенных поворотных изомеров для всех звеньев в цепи в кристалле обеспечивает его дальнейший порядок, зная положение атомов в цепи в данном макромолекулярном звене, мы знаем их для сколь угодно удаленных звеньев, т. к. расположение атомов строго периодично. Вместе с тем в кристалле имеется и ближний порядок: определенное расположение соседних звеньев. При плавлении и растворении полимера дальний порядок исчезает, но ближний порядок сохраняется. Сохранение ближнего порядка в макромолекуле следует из того, что кристаллические структуры полимеров соответствуют минимуму потенциальной энергии. Исходя из этих соображений, Птицын и Шаронов предположили, что ближний одномерной порядок в свободной макромолекуле, образующей статклубок, аналогичен дальнему одномерному порядку в кристалле. Это подтвердилось в исследованиях по оптики и спектроскопии. Она легла в основу более точных расчетов физических свойств макромолекул, исходящих из ПИТ. ПИТ дает молекулярное истолкование растяжению полимера и предсказывает, что наряду с энтропийной упругостью должна быть и энергетическая, поскольку разность энергий ротамеров 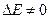, значит должна быть отличной от 0 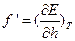, причем 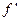зависит от 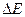. Это подтвердилось экспериментально.

Итак, гибкость полимера (сворачивание гибкой цепи в клубок) определяется ее термодинамической гибкостью, чем больше гибкость, тем меньше 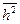при заданных 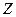и 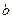. В растворе наиболее вероятная конформация полимера – свернутый клубок, в котором энтропия системы максимальна. При растяжении полимера происходит развертывание клубка и уменьшение числа возможных конформаций, что сопровождается уменьшением энтропии.

Набухание макромолекулы в результате проникновения растворителя внутрь клубка, подобно растяжению каучука, также переводит ее в менее вероятную конформацию. Возникающая при этом упругая сила энтропийной природы в конце концов приводит к тому, что набухание прекращается. Это явление лежит в основе эластичности полимеров типа каучука.