V. Теория Мора

Согласно теории Мора, два напряженных состояния равноопасны, если для соответствующих двух главных напряжений 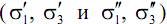соблюдается соотношение

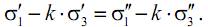
Отсюда вытекает формула для эквивалентного напряжения:

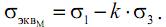
Здесь коэффициент k представляет собой отношение предельных напряжений при одноосном растяжении и при одноосном сжатии. Если принять, что коэффициенты запаса прочности по отношению к предельным напряжениям растяжения и сжатия одинаковы, то k можно определить из выражения:

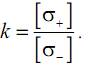
Окончательно условие прочности по теории Мора запишется следующим образом

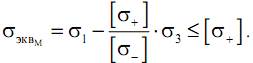
Теория прочности Мора позволяет установить сопротивление разрушению материалов, обладающих разными сопротивлениями растяжению и сжатию. Как видим, гипотеза Мора (как и III теория) не учитывает влияния промежуточного главного напряжения σ2 – это несомненный ее недостаток. Опыты показывают, что достаточно точные результаты гипотеза Мора дает для напряженных состояний смешанного типа, то есть для тех случаев, когда σ1 и σ3 имеют разные знаки.

Таким образом, для практических расчетов следует рекомендовать четвертую (или третью) теории прочности для материалов, одинаково сопротивляющихся растяжению и сжатию, и теорию Мора – для материалов, различно сопротивляющихся растяжению и сжатию, то есть для хрупких материалов (для них в настоящее время пока еще применяют и вторую теорию прочности).