Конформационная теория макромолекул
В 1951г. В.М.Волькенштейн выдвинул теорию поворотно-изомерного строения биополимеров. Он предложил заменить непрерывную функцию 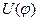 разрывной в соответствии с набором дискретных поворотных состояний. Такое приближение оправдано, когда минимумы энергии разделены барьерами, величина которых существенно больше
разрывной в соответствии с набором дискретных поворотных состояний. Такое приближение оправдано, когда минимумы энергии разделены барьерами, величина которых существенно больше 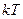 . На основе поворотно-изомерной теории, зная энергии различных поворотных изомеров, можно вычислить вероятность определенной конформации молекулы.
. На основе поворотно-изомерной теории, зная энергии различных поворотных изомеров, можно вычислить вероятность определенной конформации молекулы.
Вращательная статсумма i-ой связи, определяемая интегралом: 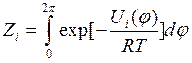 в поворотно-изомерном приближении заменяется на сумму из
в поворотно-изомерном приближении заменяется на сумму из 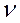 членов, где
членов, где 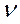 - число поворотных изомеров данной i-связи:
- число поворотных изомеров данной i-связи: 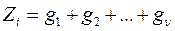 , где
, где 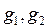 и т.д. статистические веса, характеризующие изомеры i-ой связи. Они равны
и т.д. статистические веса, характеризующие изомеры i-ой связи. Они равны 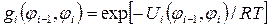 .
.
Статистический вес конфигурационной цепи в целом выражается следующим образом:
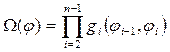 , где учтены изомеры уже всех n-связей в цепи. Полная конфигурационная статсумма для всей цепи формально выражается следующим образом:
, где учтены изомеры уже всех n-связей в цепи. Полная конфигурационная статсумма для всей цепи формально выражается следующим образом:
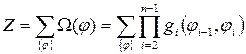 , где суммирование ведется по всем конфигурациям.
, где суммирование ведется по всем конфигурациям.
Статвес 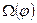 конфигурации
конфигурации 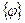 определяет частоту, с которой она встречается в равновесном статансансамбле молекул. Вероятность
определяет частоту, с которой она встречается в равновесном статансансамбле молекул. Вероятность 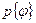 того, что данная молекула обладает именно данной конфигурацией, равна статистическому весу этой конфигурации, деленному на статсумму всех возможных конфигураций, т.е. определяется так:
того, что данная молекула обладает именно данной конфигурацией, равна статистическому весу этой конфигурации, деленному на статсумму всех возможных конфигураций, т.е. определяется так:
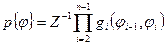 .
.
Вычисление статсуммы обычными способами оказывается весьма трудоемким, но может быть проведено матричными методами. Члены суммы состоят из произведений типа 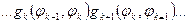 , в которых первый индекс каждого множителя должен совпадать со вторым индексом предшествующего ему в произведении множителя. Величины статвесов
, в которых первый индекс каждого множителя должен совпадать со вторым индексом предшествующего ему в произведении множителя. Величины статвесов 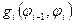 можно рассматривать как элементы некоторой матрицы:
можно рассматривать как элементы некоторой матрицы: 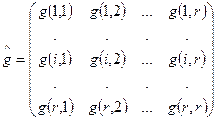 , где элементы матрицы
, где элементы матрицы 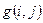 суть статистические веса соответствующих изомеров.
суть статистические веса соответствующих изомеров.
Математические вычисления показывают, что статсумма Z аппроксимируется выражением: 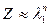 , при n >>1, где
, при n >>1, где 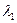 - максимальное собственное число матрицы
- максимальное собственное число матрицы 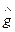 . Из равенства
. Из равенства 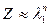 используя обычные выражения статфизики, можно, например, найти значение свободной энергии:
используя обычные выражения статфизики, можно, например, найти значение свободной энергии: 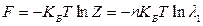 , или внутренней энергии системы
, или внутренней энергии системы
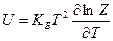 .
.
Дата добавления: 2015-02-07; просмотров: 1283;
