Статистическая обработка результатов прямых измерений

Статистическая обработка результатов измерений рассмотрена во многих литературных источниках. Корректное выполнение статистической обработки «исправленных» результатов измерений заключается в строгом соблюдении требований действующей метрологической нормативной документации (ГОСТ 8.207-76, МИ 1317-86 и др.).

Подготовка массива результатов измерений к статистической обработке заключается в «исправлении результатов измерений». Задача-максимум состоит в исключении из результатов измерений всех систематических составляющих, задача минимум – в исключении переменных систематических составляющих. Следует признать, что любое исключение погрешностей не бывает абсолютным; в результатах могут содержаться невыявленные систематические составляющие, а также всегда остаются неисключенныеостаткисистематическихпогрешностей.

Рассмотрим порядок статистической обработки исправленных результатов прямых равнорассеянных измерений одной и той же величины.

1. Расчет среднего арифметического значения X_ср(получение точечной оценки результата измерения)

.

2. Расчет отклоненийV_i результатов наблюдений от среднего арифметического

.

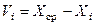3. Расчет оценки СКО результатов наблюдений

.

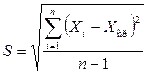4. Проверка гипотезы о сходимости эмпирического и теоретического распределений по критериям согласия.

При n > 50 для проверки принадлежности распределения к нормальному предпочтительно использование критериев Пирсона c² или Мизеса-Смирнова w². При 50 > n > 15 для проверки принадлежности распределения к нормальному предпочтительным является составной критерий (принятое условное обозначение W).

Проверки по критериям согласия проводят при уровнях значимости q от 10 % до 2 %. Принятые значения уровней значимости приводят в описании методики выполнения измерений или обработки результатов измерений.

При n ≤ 15 проверку принадлежности распределения к нормальному не проводят, а качественную оценку формируют на основе априорной информации о виде (законе) распределения случайной величины, что позволяет затем перейти к соответствующей количественной оценке.

5. Статистическая проверка наличия результатов с грубыми погрешностями.

При нормальном распределении погрешностей можно применять упрощенную процедуру отбраковывания экстремальных отклонений, например, по критерию 3s

|V_extr| > 3s.

Соблюдение неравенства позволяет утверждать, что проверяемый результат содержит грубую погрешность и должен исключаться из рассмотрения. Если отбракован хотя бы один результат с грубой погрешностью обработка повторяется с п.1.

6. Расчет оценки среднего квадратического отклонения результата измерения (оценки СКО среднего арифметического значения)

__

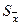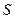= √n .

7. Расчет значения границы погрешности результата измерения Δ (по модулю)

Δ = t ,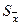

где t – коэффициент Стьюдента, зависящий от числа результатов наблюдений n и принятой доверительной вероятностиР;

Р – доверительная вероятность.

Обычно принимают доверительную вероятность Р = 0,95 или (в особых случаях) 0,99 и выше. Особые случаи – те, в которых результаты измерений связаны со здоровьем и безопасностью жизни людей, с возможными значительными экономическими потерями и т.д.

8. Запись результата измерения A в установленной форме

Q = X_ср ± Δ, Р,

где X_ср– точечная оценка результата измерений, рассчитанная как среднее арифметическое значение для всей серии наблюдений;

Δ – доверительная граница результата измерений, которую рассчитывают с использованием зависимостей

Δ = t ,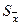

гдеt – коэффициент Стьюдента;

В случае наличия значимых неисключенных систематических составляющих погрешности значения границ погрешности результата измерения определяют в соответствии с требованиями ГОСТ 8.207.