Классификация измерений

Под измерением некоторого свойства можно понимать получение оценки этого свойства при сопоставлении измеряемой величины с единицей, воспроизводимой мерой (непосредственное воспроизведение) или прибором (опосредованное воспроизведение).

Измерение физической величины (ФВ) –совокупность операций по применению технического средства, хранящего единицу ФВ, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения этой величины.

Основное уравнение измерения физической величины можно записать в виде

Q = Nq,

где Q – измеряемая физическая величина;

q – единица физической величины;

N – числовое значение физической величины (определяет соотношение измеряемой величины и использованной при измерениях единицы.

Из уравнения измерения следует, что в основе любого измерения лежитсравнение исследуемой ФВ с аналогичной величиной определенного размера, принятой за единицу, что обеспечивает нахождение соотношения только в явном виде. Суть измерения состоит в определении числового значения ФВ. Этот процесс называют измерительным преобразованием, подчеркивая связь измеряемой ФВ с полученным числом. Можно представить однократное преобразование или цепочку преобразований измеряемой ФВ в иную величину, но конечной целью преобразования является получение числа (рис. 2.1). Измерительное преобразование всегда осуществляется с использованием некоторого физического закона или эффекта, который рассматривают как принцип, положенный в основу измерительного преобразования (принцип измерения). Под принципом измерений понимают физическое явление или эффект, положенное в основу измерений.

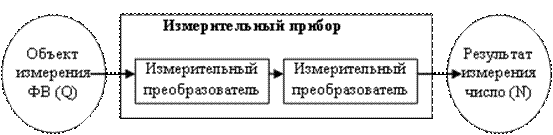
Рис. 2.1. Измерение как преобразование измеряемой

физической величины в число

Как примеры можно рассмотреть измерение температуры с помощью термопары (использование термоэлектрического эффекта), измерение массы взвешиванием на пружинных весах (определение искомой массы по пропорциональной ей силе тяжести, основанное на принципе пропорциональной упругой деформации).

Для систематизации подхода к измерению, прежде всего, необходимо классифицировать сами измерения.

Видом измеренийназвана часть области измерений, имеющая свои особенности и отличающаяся однородностью измеряемых величин.

Систематизацию видов измерений можно осуществлять по следующим классификационным признакам:

· прямые и косвенные измерения;

· совокупные и совместные измерения;

· абсолютные и относительные измерения;

· однократные и многократные измерения;

· статические и динамические измерения;

· равноточные и неравноточные измерения;

Прямые и косвенные измерения различают в зависимости от способа получения результата измерений. Прямое измерение– измерение, при котором искомое значение ФВ получают входе измерений непосредственно, например, определяют по устройству отображения измерительной информации применяемого средства измерений. Формально без учета погрешности прямые измерения могут быть описаны выражением

Q = х,

где Q – измеряемая величина,

х – результат измерения.

Косвенное измерение – определение искомого значения ФВ на основании результатов прямых измерений других ФВ, функционально связанных с искомой величиной.

При косвенных измерениях искомое значение величины рассчитывают на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. Формальная запись такого измерения

Q = F (X, Y, Z,…),

где X,Y,Z,… – результаты прямых измерений.

Принципиальной особенностью косвенных измерений является необходимостьобработки результатов внеприбора (на бумаге, с помощью калькулятора или компьютера), в противоположность прямым измерениям, при которых прибор выдает готовый результат. Классическими примерами косвенных измерений можно считать нахождение значения угла треугольника по измеренным длинам сторон, определение площади треугольника или другой геометрической фигуры и т.п. Один из наиболее часто встречающихся случаев применения косвенных измерений – определение плотности материала твердого тела. Например, плотность ρ тела цилиндрической формы определяют по результатам прямых измерений массы т, высоты h и диаметра цилиндра d, связанных с плотностью уравнением

ρ = т/0,25π d² h.

Прямые и косвенные измерения характеризуют измерения некоторой одиночной ФВ. Измерение любого множества физических величин классифицируется в соответствии с однородностью или неоднородностью измеряемых величин. На этом и построено различение совокупных и совместных измерений.

Совокупные измерения – проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях.

Реально к совокупным измерениям следует отнести те, при которых осуществляется измерение нескольких одноименных величин, например, длин L₁, L₂,L₃ и т.д. Подобные измерения выполняют на специальных устройствах (измерительных установках) для одновременного измерения ряда геометрических параметров деталей.

Совместные измерения – проводимые одновременно измерения двух или нескольких неодноименных величин для определения зависимости между ними. Под совместными измерениями обычно подразумевают измерения нескольких неодноименных величин (X, Y, Z и т.д.) без последующего поиска связывающих их зависимостей. Примерами таких измерений могут быть комплексные измерения электрических, силовых и термодинамических параметров электродвигателя, измерения параметров движения и состояния транспортного средства (скорость, запас горючего, температура двигателя и др.).

Для отображения результатов, получаемых при измерениях, могут быть использованы разные оценочные шкалы, в том числе градуированные в единицах измеряемой ФВ, либо в некоторых относительных единицах. В соответствии с этим принято различать абсолютныеиотносительные измерения.

Абсолютное измерение – измерение, основанное на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант. Например, измерение силы F =mg основано на измерении основной величины – массы m и использовании физической постоянной g в точке измерения массы. Понятие абсолютное измерение применяется как противоположное понятию относительное измерение и рассматривается как измерение величины в предусмотренных для неё единицах.

Относительное измерение – измерение отношения величины к одноименной величине, играющей роль единицы, или измерение изменения величины по отношению к одноименной величине, принимаемой за исходную. Примерами таких измерений являются измерения относительной влажности, относительного удлинения.

По числу повторных измерений одной и той же величины различают однократные и многократныеизмерения.

Однократное измерение – измерение, выполненное один раз.

Многократное измерение – измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, т.е. состоящее из ряда однократных измерений.

В зависимости от поставленной цели число повторных измерений может колебаться в широких пределах (от двух измерений до нескольких десятков и даже сотен). Многократные измерения проводят или для «страховки» от грубых погрешностей (в таком случае достаточно трех-пяти измерений) или для последующей математической обработки результатов (с последующими расчетами средних значений, статистической оценкой отклонений и других параметров и характеристик). Многократные измерения называют также «измерения с многократными наблюдениями».

Статическое измерение – измерение ФВ, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения.

Динамическое измерение – измерение изменяющейся по размеру ФВ.

Динамические измерения наиболее логично рассматривать в зависимости от скорости получения средством измерения входного сигнала измерительной информации. При измерении в статическом режиме (или квазистатическом режиме) скорость изменения входного сигнала несоизмеримо ниже скорости его преобразования в измерительной цепи, и результаты фиксируются без динамических искажений. При измерении в динамическомрежиме появляются дополнительные динамические погрешности, связанные со слишком быстрым изменением либо самой измеряемой ФВ, либо входного сигнала измерительной информации, поступающего от постоянной измеряемой величины. Режим измерений могут в значительной степени определить применяемые средства измерений, например, измерение температуры с помощью ртутного термометра может быть причиной динамических погрешностей, поскольку оно несоизмеримо медленнее измерений электронными термометрами.

По реализованной точности и по степени рассеяния результатов при многократном повторении измерений одной и той же величины различают равноточные и неравноточные, а также равнорассеянные и неравнорассеянные измерения.

Равноточные измерения – ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений в одних и тех же условиях.

Неравноточные измерения – ряд измерений какой-либо величины, выполненных различающимися по точности средствами измерений и (или) в разных условиях.

Оценка равноточности и неравноточности результатов измерений зависит от выбранных значений предельных расхождений точности в сериях измерений. Допустимые расхождения оценок устанавливают в зависимости от задачи измерения. Равноточными называют серии измерений 1 и 2, для которых оценки погрешностей D₁ и D₂ можно считать практически одинаковыми

(D₁ » D₂),

а к неравноточным относят серии с различающимися погрешностями

(D₁ ¹ D₂).

Серии измерений считают равнорассеянными или неравнорассеянными по практическому совпадению или различию оценок случайных составляющих погрешностей измерений сравниваемых серий 1 и 2.

Формально это можно представить как 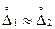или .

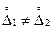По планируемой точности измерения делят на технические и метрологические. Общепринятой трактовки такого разделения в литературе нет, поэтому можно предложить логическое обоснование подобных видов измерений.

К техническимследует относить те измерения, которые выполняют с заранее установленной точностью. Иными словами,при технических измерениях погрешность измерения D не должна превышать заранее заданного значения [D]:

D £ [D],

где [D] – допустимая погрешность измерения.

Именно такие измерения наиболее часто осуществляются в производстве, откуда и произошло их наименование.

Метрологические измерениявыполняют с максимально достижимой точностью, добиваясь минимальной (при имеющихся ограничениях) погрешности измерения D, что можно записать как

D® 0.

Такие измерения имеют место при эталонировании единиц, при выполнении уникальных исследований.

Общность подхода к этим видам измерений состоит в том, что при любых измеренияхопределяютзначенияD, без чего невозможна достоверная оценка результатов.

Метод измерений– прием или совокупность приемов сравнения измеряемой физической величины с ее единицей в соответствии с реализованным принципом измерений. Метод измерений обычно обусловлен конструкцией средств измерений (СИ).

Фактически единственное принципиальное различие методов измерений в рамках стандартных терминов, это деление их на две следующие разновидности широко используемых в метрологической практике:

· метод непосредственной оценки;

· метод сравнения с мерой;

Различия между этими двумя методами измерений заключаются в том, что метод непосредственной оценки реализуют с помощью приборов без дополнительного применения мер, а метод сравнения с мерой предусматривает обязательное использованиеовеществленноймеры, которая в явном виде воспроизводит с выбранной точностью физическую величину определенного размера.

Метод непосредственной оценки – метод измерений, при котором значение величины определяют непосредственно по показывающему средству измерений.

Суть метода непосредственной оценки,как любого метода измерения состоит в сравнении измеряемой величины с мерой, принятой за единицу, но в этом случаемера «заложена» в измерительный приборопосредованно.Прибор осуществляет преобразование входного сигнала измерительной информации, после чего и происходит оценка ее значения, соответствующего всейизмеряемойвеличине

Формальное выражение для описания метода непосредственной оценки может быть представлено в следующей форме:

Q=х,

где Q– измеряемая величина,

х– показания средства измерения.

Метод сравнения с мерой– метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой.

Методхарактеризуется тем, что прибор фактически используют для определения разности измеряемой величины и известной величины, воспроизводимой мерой. Для реализации этого метода пригодны приборы с относительно небольшими диапазонами показаний, вплоть до вырожденной шкалы с одной нулевой отметкой. Примерами этого метода являются измерения массы на рычажных весах с уравновешиванием объекта гирями (мерами массы), измерения напряжения постоянного тока прибором-компенсатором путем сравнения с известной ЭДС нормального элемента.

Формально метод сравнения с мерой может быть описан следующим выражением:

Q = х + Х_м,

где Q– измеряемая величина,

х– показания средства измерения,

Х_м– величина, воспроизводимая мерой.

Метод сравнения с мерой реализуется в некоторых разновидностях:

· дифференциальный и нулевой методы измерений,

· метод совпадений,

· метод измерений замещением и метод противопоставления,

· метод измерений дополнением.

Дифференциальный метод измерений – метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами.

Фактически это метод сравнения с мерой, в котором на измерительный прибор воздействует разность измеряемой величины и величины, воспроизводимой мерой, что формально соответствует соотношению х ≠ 0в выражении

Q = х + Х_м,

Нулевой метод измерений – метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля.

Если формально это представить через х ≈0 в том же уравнении, можно записать:

Q ≈Х_м.

В качестве примера можно привести измерения массы взвешиванием на равноплечих рычажных весах с полным уравновешиванием чашек.

Метод совпадений – это метод сравнения с мерой, в котором значение измеряемой величины оценивают, используя совпадение ее с величиной, воспроизводимой мерой (т.е. с фиксированной отметкой на шкале ФВ). Для оценки совпадения можно использовать прибор сравнения или органолептику, фиксируя появление определенного физического эффекта (стробоскопический эффект, совпадение резонансных частот, плавление или застывание индикаторного вещества при достижении определенной температуры и другие физические эффекты).

В зависимости от одновременности или неодновременности воздействия на прибор сравнения измеряемой величины и величины, воспроизводимой мерой, различают метод измерений замещением и метод противопоставления.

Метод измерений замещением(метод замещения) – метод сравнения с мерой, в котором измеряемую величину замещают мерой с известным значением величины. Примером может служить взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов.

Для линейно-угловых измерений, рассматривают альтернативную пару: методы замещения и противопоставления. В этом случае метод замещения – метод сравнения с мерой, в котором известную величину, воспроизводимую мерой, после настройки прибора замещают измеряемой величиной, то есть эти величины воздействуют на прибор последовательно. Метод противопоставления – метод сравнения с мерой, в котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения, с помощью которого устанавливают соотношение между этими величинами.

Метод измерений дополнением(метод дополнения) – метод сравнения с мерой, в котором значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению. Метод может быть реализован как при замещении, так и при противопоставлении измеряемой величины и меры.

В качестве классификационного признака можно рассматривать наличие или отсутствие контакта между СИ и объектом измерений.

Контактный метод измерений– метод измерений, основанный на том, что чувствительный элемент прибора приводится в контакт с объектом измерения.

Бесконтактный метод измерений – метод измерений, основанный на том, что чувствительный элемент средства измерений не приводится в контакт с объектом измерения. Примерами могут быть измерение температуры в доменной печи пирометром и измерение расстояния до объекта оптическими средствами.

При механическом контакте чувствительного элемента средства измерений с объектом, необходимо учитывать деформации из-за их недостаточной жесткости элементов, контактные деформации, и др. При отсутствии механического контакта следует учитывать особенности «бесконтактного съема» измерительной информации – оптические искажения в воздухе, ослабление сигнала на расстоянии, наличие пыли и масляных пленок на поверхности объекта и др.

<10 11 121314 15 16 >

Дата добавления: 2015-02-05; просмотров: 1634;