Результатов

Понятие «неопределенность», как наименование количественно оцениваемого свойства измерения, является относительно новым в метрологии. Термин «неопределенность» введен «Руководством по предоставлению неопределенности измерений» (далее «Руководство»), поскольку «погрешность» – идеализированное понятие и не может быть известна точно.

Неопределенность (измерения) есть параметр, связанный с результатом измерения, характеризующий дисперсию значений, которые могли быть обоснованно приписаны измеряемой величине.

Руководство устанавливает общие правила оценивания и выражения неопределенности измерения, которые следует соблюдать при любых уровнях точности в широком спектре измерений, включая:

· измерения для обеспечения контроля качества и поддержания заданного уровня качества в процессе производства;

· измерения в ходе фундаментальных и прикладных исследований;

· измерения калибровочных мер;

· измерения с целью обеспечения единства измерений в стране;

· измерения для разработки, поддержания и сличения международных и национальных эталонов единиц физических величин, включая стандартные образцы свойств веществ и материалов.

К оцениванию неопределенности следует приступать только после исключения результатов с грубыми погрешностями и исправления результатов измерений (исключения систематических составляющих погрешностей). Такой подход позволяет обоснованно применять математический аппарат теории вероятностей и математической статистики к «исправленным результатам измерений.

Неопределенность измерения в некоторых информационных источниках трактуется как мера возможной погрешности оцененного значения измеряемой величины, либо как оценка, характеризующая диапазон значений, в пределах которого находится истинное значение измеряемой величины. Под неопределенностью измерений фактически подразумевают то, что результат измерений фиксируется интервалом значений, а не конкретной точкой на числовой оси физической величины, при этом координата истинного значения остается неизвестной (неопределенной). В более широком смысле можно говорить также и о неопределенности «закона распределения» результатов многократных наблюдений при измерении конкретной физической величины. Графическое отображение неопределенности представлено на рис. 2.8.

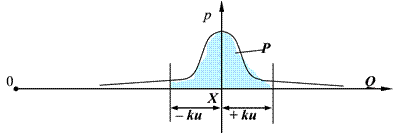
Рис. 2.8. Графическая интерпретация неопределенности измерений

при нормальном распределении случайной погрешности

На рисунке отражены качественная оценка неопределенности (нормальное распределение), а также ее количественные оценки (расширенная неопределенность 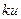при выбранной доверительной вероятности Р).

В Руководстве используются следующие термины и определения:

Стандартная неопределенность – неопределенность результата измерения, выраженная как стандартное отклонение.

Оценка (неопределенности) по типу А – метод оценивания неопределенности путем статистического анализа рядов наблюдений.

Оценка (неопределенности) по типу В – метод оценивания неопределенности иным способом, чем статистический анализ рядов наблюдений.

Суммарная стандартная неопределенность – стандартная неопределенность результата измерения, когда результат получают из значений ряда других величин, равная положительному квадратному корню суммы членов, причем члены являются дисперсиями или ковариациями этих других величин, взвешенными в соответствии с тем, как результат измерения изменяется в зависимости от изменения этих величин.

Расширенная неопределенность – величина, определяющая интервал вокруг результата измерения, в пределах которого можно ожидать, находится большая часть распределения значений, которые с достаточным основанием могли быть приписаны измеряемой величине.

Коэффициент охвата – числовой коэффициент, используемый как множитель суммарной стандартной неопределенности для получения расширенной неопределенности. При нормальном распределении обычно применяют значения коэффициента охвата k, называемого также «коэффициент покрытия» в диапазоне от 2 до 3.

Установление связи между выбранным уровнем доверия и интервалом, характеризующим расширенную неопределенность, требует явных и неявных предположений относительно закона распределения вероятностей.

Классификация методов оценивания неопределенности на тип А и тип В представляет два различных способа получения оценки составляющих неопределенности. Оба типа основаны на вероятностном оценивании распределений случайных величин, а составляющие неопределенности при любом типе оценивания количественно представляют как оценки дисперсией или стандартных отклонений. Различия двух типов оценивания заключаются в методе получении оценки: прямое получение оценки путем статистического анализа рядов наблюдений (оценивание неопределенности по типу А), или получение оценки без непосредственного статистического анализа рядов наблюдений (оценивание неопределенности по типу В). Стандартную неопределенность при оценивании по типу В получают из предполагаемой функции плотности вероятностей, причем используют готовые оценки, полученные в ходе разнообразных метрологических мероприятий.

Наиболее распространенным способом формализации неполного знания о распределении величины является постулирование равновероятного распределениявозможных значений этой величины в указанных границах.

Расширенную неопределенность Uполучают умножением суммарной стандартной неопределенности u, на коэффициент охвата k. Фактически U представляет собой доверительный интервал, который с выбранной вероятностью накрывает истинное значение измеряемой величины. Коэффициент охвата k зависит от вида приписанного распределения и выбранной доверительной вероятности.

По определению суммарная стандартная неопределенность измерения, представляет собой оценку среднего квадратического отклонения результата косвенных измерений, посколькурезультатизмеренияполучают из значений ряда других величин.Суммарную стандартную неопределенность при этом рассчитывают как значение квадратного корня из суммы дисперсий (или ковариаций) этих величин с учетом весовых коэффициентов.

Фактически понятие«суммарная стандартная неопределенность» следует рассматривать в двух вариантах:

· оценка неопределенности прямых измерений, получаемая «суммированием» нескольких составляющих, например, вызванных наличием погрешности применяемого прибора, погрешностей всех использованных мер и субъективной погрешности (при условии отсутствия методической составляющей и проведении измерений в нормальных условиях);

· оценка неопределенности косвенных измерений, получаемая «суммированием» составляющих погрешностей результатов прямых измерений, входящих в функциональную зависимость для расчета результата косвенных измерений.

Значения составляющих, входящих в суммарную неопределенность, могут быть получены путем оценивания как по типу А, так и по типу В, главное требование – под корнем эти составляющие должны быть представлены оценками соответствующих дисперсий.