Вычисление стандартной неопределенности (uB) по типу В

Исходными данными для вычисления является следующая информация:

· данные предшествовавших измерений величин, входящих в уравнение измерения; сведения о виде распределения вероятностей;

· данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих приборов и материалов;

· неопределенности констант и справочных данных;

· данные поверки, калибровки, сведения изготовителя о приборе и др.

Неопределенности этих данных обычно представляют в виде границ отклонения значений величины от ее точечной оценки. При неполном знании о неопределенности некоторой i-й входной величины обычно постулируют равновероятное распределение возможных значений этой величины в указанных (нижней и верхней) границах [b_i-, b_i+]. При этом стандартную неопределенность, вычисляемую по типу В, определяют поформуле:

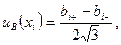
а для симметричных границ (± b_i) –

.

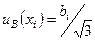В случае других законов распределения формулы для вычисления неопределенности по типу В будут иными.

Для вычисления коэффициента корреляции используют согласованные пары результатов измерений (x_il, x_jl) (l=1,…n_ij), где n_ij – число согласованных результатов измерений:

.

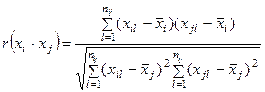Вычисление суммарной стандартной неопределенности (u_c)

В случае некоррелированных результатов измерений x₁,…, x_m оценку дисперсии суммарной стандартной неопределенности вычисляют по формуле:

.

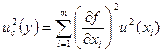В случае коррелированных результатов измерений x₁,…, x_m оценку дисперсии суммарной стандартной неопределенности вычисляют по формуле:

,

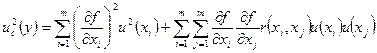где r(x_i, x_j)– коэффициент корреляции,

u(x_i) – стандартная неопределенность входной величины i, вычисленная по

типу А или по типу В.

Выбор коэффициента охвата k при вычислении расширенной неопределенности

В общем случае коэффициент охвата выбирают в соответствии с формулой:

k = t_p(v_eff),

где t_p(v_eff) – квантиль распределения Стьюдента с эффективным числом степеней свободы v_eff и доверительной вероятностью (уровнем доверия) р.

Число степеней свободы определяют по формуле:

,

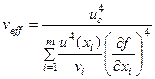где v_i – число степеней свободы при определении оценки i-й входной величины:

v_i = n_i – 1 для вычисления неопределенностей по типу А;

v_i =∞ – для вычисления неопределенностей по типу В.

Во многих практических случаях при вычислении неопределенностей измерений делают предположение о нормальном законе распределения возможных значений измеряемой величины и полагают:

k = 2 при р ≈ 0,95 и k = 3 при р ≈ 0,99.

При допущении распределения данных по закону равной вероятности полагают:

k = 1,65 при р ≈ 0.95 и k = 1,71 при р ≈ 0,99.

При представлении результатов измерений Руководство рекомендует приводить достаточное количество информации для возможности проанализировать или повторить весь процесс получения результата измерений и вычисления неопределенностей измерений, а именно:

· алгоритм получения результата измерений.

· алгоритм расчета всех поправок и их неопределенностей;

· неопределенности всех используемых данных и способы их получения:

· алгоритмы вычисления суммарной и расширенной неопределенностей (включая значение коэффициента k).