Проектирование ФНЧ на сосредоточенных элементах
Проектирование фильтрующих цепей на основе линий передачи, как правило, начинают с рассмотрения фильтра, состоящего из сосредоточенных пассивных элементов. Выбранный соответствующим образом фильтр на сосредоточенных элементах обычно синтезируется с помощью таблиц. Электрические характеристики такого фильтра на сосредоточенных элементах, значение которых определены по таблицам, примерно совпадают с заданными при синтезе.
Далее по найденным значениям сосредоточенных элементов определяются значения элементов с распределенными параметрами. Необходимые для этого преобразования рассмотрим ниже. В данном разделе основное внимание уделено простым вычислительным программам, освобождающим разработчика от обращения к таблицам.
Рассматриваются фильтры нижних частот (ФНЧ) с двумя различными частотными характеристиками. Будет показано, как синтезированный прототип фильтра нижних частот с помощью несложных преобразований превратить в прототип фильтра верхних частот или полосового фильтра.
Фильтр нижних частот представляет собой частотно-избирательную цепь с полосой пропускания от нулевой частоты до некоторой частоты среза ωcp. Амплитудно-частотную характеристику (АЧХ) идеального ФНЧ (рис. 3.1, а), реализовать на практике невозможно из-за бесконечно большой крутизны характеристики на частоте ωcp, но приблизиться к которой можно различными способами. Один из них заключается в аппроксимации АЧХ передаточной функцией, впервые предложенной Баттервортом [1] и описывающей зависимость коэффициента передачи от частоты:
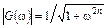 , n=1,2,3,... (3.1)
, n=1,2,3,... (3.1)
Фильтры с частотной характеристикой, соответствующей (3.1), получили название фильтров с характеристикой Баттерворта, или с максимально плоской характеристикой, поскольку на частотах, много меньших частоты среза, коэффициент передачи таких фильтров практически не зависит от частоты.
Другой хорошо известный способ аппроксимации состоит в описании АЧХ фильтра следующей передаточной функцией:
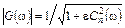 , n=1,2,3,…, (3.2)
, n=1,2,3,…, (3.2)
где ε – константа; Сn(ω) – полиномы Чебышева первого рода порядка n, описываемые выражениями
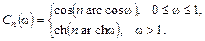 (3.3)
(3.3)
Из 3.3 следует
С0(ω)= 1, C1(ω)=ω.
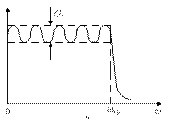
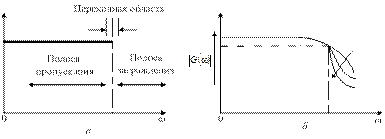
Рис. 3.1. Идеальная (а), максимально плоская (б), Чебышевская (в) АЧХ фильтра нижних частот
Полином Чебышева вычисляют обычно не по формуле (3.3), а с помощью рекуррентного соотношения, для записи которого удобно ввести обозначение θ= ar cos ω при 0 ≤ ω ≤ 1.
Тогда
Сn(ω) = cos (nθ),
Cn+1(ω) = cos[(n + l)θ] = cos(nθ)cosθ - sin(nθ) sinθ,
Cn1(ω)) = cos[(n - 1)θ] = cos(nθ)cosθ + sin(nθ) sinθ.
Складывая два последних равенства, получаем искомое рекуррентное соотношение
Сn+1 (ω) + Cn1(ω) = 2cos(nθ)cosθ = 2ωСn (ω),
откуда следует
С2(ω) = 2ωC1(ω) - С0(ω) = 2ω2 - 1.
Именно так составлена таблица полиномов Чебышева первого рода (табл. 3.1).
Таблица 3.1
Полиномы Чебышева 1-го рода
| Порядок n | Полином Cn(w) |
| w | |
| 2w2 - 1 | |
| 4w3 - 3w | |
| 8w4 - 8w2+1 | |
| 16w5 - 20w3+5w | |
| 32w6 - 48w4+18w2-1 |
В полосе пропускания характеристика типичной чебышевской АЧХ фильтра нижних частот (см. рис. 3.1, в) носит осциллирующий характер с неизменной амплитудой осцилляции. Поэтому такие фильтры иногда называют фильтрами с постоянной амплитудой осцилляции. Амплитуда осцилляции в полосе пропускания связана с крутизной характеристики на частотах выше ωср: если при неизменном числе звеньев фильтра увеличивать крутизну характеристики в полосе заграждения, то одновременно возрастает амплитуда осцилляции. Лишь изменяя число звеньев в фильтре, можно изменять крутизну характеристики при неизменной амплитуде осцилляции. По сравнению с фильтрами нижних частот Баттерворта аналогичные чебышевские фильтры имеют явное преимущество в полосе заграждения: при одинаковом числе реактивных элементов последние позволяют получить большую крутизну характеристики, чем первые.
Увеличение числа реактивных элементов приводит к увеличению нелинейности фазочастотных характеристик (ФЧХ) фильтров этих типов. По сравнению с ФЧХ соответствующего чебышевского фильтра ФЧХ фильтра Баттерворта обладает большей линейностью. В случае, когда начинают доминировать требования к линейности фазовой характеристики проектируемого фильтра, преимущества чебышевского фильтра могут оказаться не столь существенными из-за недопустимой нелинейности его ФЧХ. Если линейность ФЧХ фильтра - главное требование, то предпочтение отдают фильтрам Бесселя, имеющим весьма линейную ФЧХ в полосе пропускания по сравнению с фильтрами Баттерворта и Чебышева, но гораздо худшую АЧХ. Фильтры Бесселя используются в фазовращателях и схемах, где требуется обеспечить заданную временную задержку проходящего сигнала [1]. Мы не рассматриваем проектирование фильтров Бесселя. Однако методика расчета фильтров Чебышева и Баттерворта может быть распространена и на эти фильтры.
Логарифмируя (3.1) и (3.2), получаем формулы для расчета вносимого фильтром затухания, выраженного в децибелах. Для фильтра с максимально плоской характеристикой:
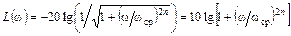 . (3.4)
. (3.4)
Для фильтра с чебышевской характеристикой:
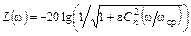 , (3.5)
, (3.5)
т. е. при 0 ≤ ω ≤ ωcp:
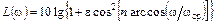 ,
,
а при ω > ωcp:
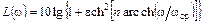 ,
,
ε = 10 (ампл. осц. в дБ)/10 -1.
В этих выражениях все частоты нормированы к частоте среза ωcp.
Обычно при синтезе необходимо по заданному значению затухания L(ω) на определенной частоте ωcp в полосе заграждения определять число звеньев в фильтре. Для решения этой задачи выразим n из (3.4) и (3.5) в явном виде:
для фильтра Баттерворта:
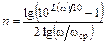 ; (3.6)
; (3.6)
для фильтра Чебышева:
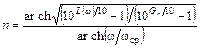 , (3.7)
, (3.7)
где Gr – амплитуда осцилляции в полосе пропускания, дБ. При вычислениях по (3.7) удобно использовать тождество
 |
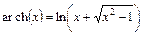 .
.
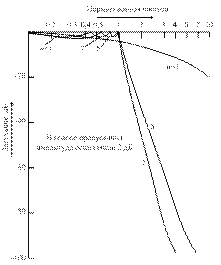
Рис. 3.2. Затухание, вносимое чебышевским фильтром при амплитуде осцилляции 2 дБ
Фильтр, как правило, располагается между генератором с известным внутренним сопротивлением и заданной нагрузкой (рис. 3.3), причем в большинстве случаев можно считать внутреннее сопротивление генератора и сопротивление нагрузки чисто активными. Такое представление весьма удобно, поскольку во многих работах, посвященных анализу и синтезу электрических цепей, схемы именно такого типа рассмотрены наиболее подробно (рис. 3.4). В схеме одного из подобных фильтров, где использованы общепринятые обозначения, параметры g связаны с корнями передаточной функции и n-звенного фильтра. При синтезе фильтра с заданной АЧХ параметры его элементов вычисляются через значения g.
Фильтр состоит из нескольких Т-образных цепей, образованных индуктивностями и емкостями. Можно построить аналогичную схему, дуальную к первой, состоящую из П-образных цепей, причем в этом случае g1 будет емкостью параллельно включенного конденсатора, a g2 – индуктивностью в последовательной цепи. Если g1 и gn – емкости, то g0 и gn+1 – соответственно активные сопротивления генератора и нагрузки, если же g1 и gn – индуктивности, то g0 и gn+1 – активные проводимости генератора и нагрузки. Существуют простые формулы для расчета g-параметров при синтезе фильтра на сосредоточенных элементах [2]. Хотя формулы достаточно просты, их использование трудоемко. Поэтому в большинстве случаев разработчики, игнорируя эти формулы, пользуются таблицами, составленными по результатам численных расчетов.
Для фильтра Баттерворта g-параметры определяются по следующим формулам:
ωcp = 1, g0 = gn+1 =1,
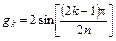 , k=1,2,3,…n,
, k=1,2,3,…n,
где аргумент синуса выражен в радианах.
Значения g распределены симметрично относительно середины фильтра, что выполняется как при четных, так и при нечетных значениях n. Поэтому включение такого фильтра между равными сопротивлениями не приведет к рассогласованию.
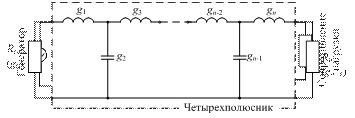 |
Рис. 3.3. Представление фильтра в виде четырехполюсника
Рис. 3.4. Фильтр нижних частот, нагруженный с обеих сторон
Для чебышевского фильтра, имеющего амплитуду осцилляции Gr, дБ, в полосе пропускания, g-параметры вычисляются по следующим формулам:
ωcp = 1, g0 = 1; ωcp = 1, g1 =2a1/ψ;
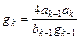 ; k = 2,3,…n;
; k = 2,3,…n;
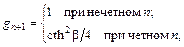
где 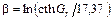 ;
; 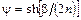 ;
;
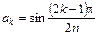 ;
; 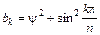 .
.
При нечетном n значение g распределено симметрично относительно середины фильтра, тогда как при четном n симметрия нарушается. Эта особенность фильтра может оказаться полезной, когда необходимо согласовывать неравные сопротивления.
Пример 3.1. Рассчитать трехзвенный ФНЧ с максимально плоской характеристикой, подключенный к генератору с внутренним сопротивлением 50 Ом и нагруженный на 50-омное сопротивление. Частота среза фильтра 10 МГц.
Решение
Начнем с расчета параметров фильтра с характеристикой Баттерворта, нормированных к 50 Ом и при ωср = 1, т. е. g - параметров:
n = 3, g0= 1, g4=1;
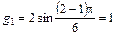 ;
; 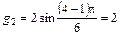 ;
;
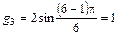 .
.
Теперь необходимо перейти к ненормированным значениям. Пусть эквивалентная схема фильтра имеет вид, показанный на рис. 3.5. Конкретные значения элементов в схеме фильтра рассчитываем через g-параметры, учитывая, что ωср = = 2p×107 рад/с и Rн = 50 Ом:
R0 = Rн g0 = 50·1 = 50 Ом; С1 = g1/(Rн ωср) = 318 пФ;
L1 = g1 Rн / ωср = 1590 нГн; С2 = g3 / (Rн ωср) = 318 пФ.
Обратите внимание на порядок расчета значений элементов схемы с помощью g-параметров и на то, что значения элементов схемы симметричны относительно индуктивности фильтра.
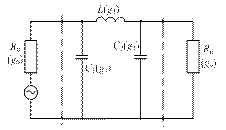 Сформулируем правила, с помощью которых проводится пересчет нормированных значений параметров (g-параметров) в конкретные значения элементов фильтра:
Сформулируем правила, с помощью которых проводится пересчет нормированных значений параметров (g-параметров) в конкретные значения элементов фильтра:
1) пересчет при заданной частоте среза Рис. 3.5. Схема фильтра к примеру 3.1
заключается в делении
каждого нормированного значения g, относящегося к конденсатору или индуктивности, на заданную ненормированную угловую частоту среза, рад/с; активные сопротивления в данной операции не участвуют;
2) пересчет по заданному значению сопротивления нагрузки Rн заключается в умножении всех g, относящихся к активным сопротивлениям и индуктивностям, на Rн и делении всех g, относящихся к емкостям, на Rн.
Дата добавления: 2015-02-03; просмотров: 4045;
