К полосовому фильтру
Переход от ФНЧ к полосовому фильтру (ПФ) основан на преобразовании идеализированных АЧХ (рис. 3.7). В данном случае необходимо выполнить следующие преобразования: частота ω1 = 1 должна перейти в частоту ωв , частота ω1 = 0 – в частоту ω0, частота ω1 = -1 – в частоту ωн.
Требуемое преобразование описывается равенством
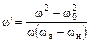 .
.
Центральная частота ПФ находится как среднее геометрическое значений ωв и ωн:
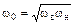 .
.
Отметим, что нагруженная добротность ПФ, граничные частоты ωв и ωн полосы пропускания которого определяются по уровню 3 дБ, рассчитывается по простой формуле
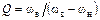 .
.
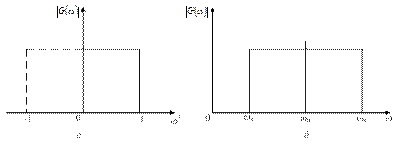 |
Рис. 3.7. Частотное преобразование, переводящее характеристику фильтра нижних частот (а) в характеристику полосового фильтра с шириной полосы пропускания ωв – ωн (б)
Формулы, применяемые при частотном преобразовании, приведены в табл. 3.2.
Таблица 3.2
Преобразования элементов фильтров
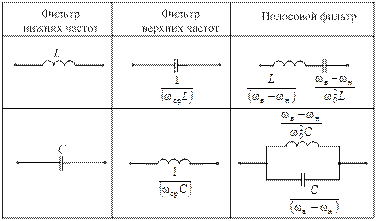 |
Амплитуда и фаза сигнала на входе и выходе фильтра различны. Изменение амплитуды обсуждалось ранее. Сигнал на выходе фильтра запаздывает по фазе, поскольку для его прохождения через фильтр необходимо определенное конечное время. Поэтому влияние фильтра на фазу проходящего сигнала можно оценивать как временем зaдepжки, так и вносимым фазовым сдвигом. В монографии Вайнберга [1] предложена методика расчета времени задержки и фазового сдвига сигналов, проходящих через n-звенные фильтры с максимально плоской и чебышевской характеристиками.
Дата добавления: 2015-02-03; просмотров: 1064;
