С распределенными параметрами
До сих пор рассматривались примеры синтеза фильтров нижних частот, выполненных на элементах с распределенными параметрами. Перейдем теперь к синтезу фильтров верхних частот на аналогичных элементах, выполнив его на основе фильтра-прототипа из сосредоточенных элементов. При рассмотрении фильтра-прототипа верхних частот на сосредоточенных элементах возникает проблема реализации последовательно включенного в линию передачи конденсатора. Самое простое решение – сделать зазор в центральном проводнике коаксиального кабеля или в полоске микрополосковой или симметричной полосковой линии. На первый взгляд такое решение очень заманчиво, однако на практике его не используют по двум причинам: во-первых, для получения требуемых значений емкости в фильтре-прототипе из сосредоточенных элементов необходимы очень малые зазоры, воспроизвести которые при изготовлении весьма трудно; во-вторых, зазор в токонесущем проводнике линии ведет себя не как чистая сосредоточенная емкость: его более точная эквивалентная схема представляет собой П-образную цепь, состоящую из последовательно и паралльно включенных емкостей. Поэтому использование таких зазоров нежелательно, пока не будут налажены их тщательный контроль и моделирование. Фильтры верхних частот, содержащие элементы с распределенными параметрами, как правило, выполняются по гибридной технологии, наряду с элементами с распределенными параметрами используются и сосредоточенные элементы, что позволяет реализовать требуемые схемные решения. Сосредоточенные конденсаторы в виде чипов, изготовленные с помощью тонкопленочной либо толстопленочной технологии, с успехом применяются на частотах до 20 ГГц. В примере 3.3 рассмотрен ФВЧ в коаксиальном исполнении, содержащий элементы как с сосредоточенными, так и с распределенными параметрами.
Пример 3.3. Рассчитать ФВЧ, состоящий из отрезков коаксиальной линии и конденсаторов. Фильтр должен быть трехзвенным с максимально плоской характеристикой, частотой среза 1 ГГц и встраиваться в линию с волновым сопротивлением 50 Ом. Внутренний диаметр внешнего проводника равен 0,762 см.
Решение
Дано: n = 3; характеристика максимально плоская; Rн = R0 = 50 Ом; ωср = 2π∙109 рад/с.
1. Выбираем топологию схемы (рис. 3.12). Рассчитываем параметры для фильтра-прототипа нижних частот:
g0=g1= g3= g4=1; g2=2.
Определяем в фильтре верхних частот:
С1=С2= 1/(2π∙109∙1∙50) = 3,2 пФ; L = 3,98нГн.
2. Задаемся значением волнового сопротивления ZbLотрезка коаксиальной линии, реализующего индуктивность L, например 100 Ом. Как видно в табл. 3.3, для реализации параллельно включаемой индуктивности удобнее всего использовать короткозамкнутый шлейф, длина которого
l=Lfλg/ZвL=Lνф/ZвL;
при воздушном заполнении линии νф = 3∙1010 см/с:
l = 3∙109×3,98∙109 /100 = 1,194 см.
3. Фильтр должен встраиваться в линию с волновым сопротивлением 50 Ом. При расчете по заданному волновому сопротивлению коаксиальной линии 50 Ом и внутреннему диаметру внешнего проводника 0,762 см получаем при воздушном заполнении диаметр центрального проводника 0,33 см. Аналогично рассчитывается диаметр центрального проводника (0,14 см) короткозамкнутого отрезка линии, реализующего индуктивность L, волновое сопротивление которого 100 Ом, εr = 1, а диаметр внешнего проводника такой же, как и для 50-омной линии.
Проектирование завершается синтезом последовательно включенных конденсаторов. Поскольку коаксиальная линия обладает осевой симметрией, удобно использовать в качестве С1 и С2 плоский конденсатор с круглыми обкладками. При расчете такого конденсатора можно пренебречь краевыми полями, если диаметр обкладок гораздо больше расстояния между ними. При этом емкость конденсатора C=ε0εrA/d, где А=pr2 – площадь обкладок; d – расстояние между ними; r – радиус обкладок.
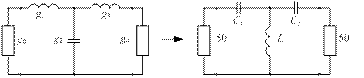 |
Рис. 3.12. Фильтр-прототип нижних частот (а) и эквивалентная схема фильтра верхних частот (б) к примеру
Чтобы подобный конденсатор помещался в коаксиальную линию, необходимо выполнение условия 0,33 < 2r < 0,762. Выберем 2r = 0,6 см, т. е. r = 0,3 см.
Выбрав заполняющий конденсатор диэлектрик εr = 2,3, рассчитаем расстояние между обкладками:
d =8,854∙10-14×2,3×π 0,32 /3,2∙10-12 = 0,018 см.
На этом проектирование заканчивается. Синтезированная конструкция фильтра показана на рис. 3.13, а ее характеристики на рис. 3.14.
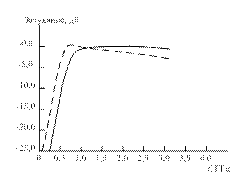
Приведена (рис. 3.14) расчетная АЧХ фильтра, спроектированного в данном примере, на нем же для сравнения нанесена АЧХ фильтра-прототипа верхних частот на сосредоточенных элементах (см. рис. 3.12, б).
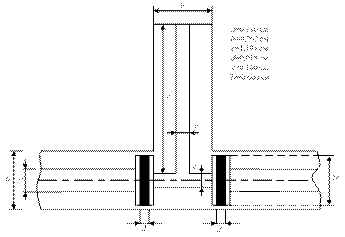 |
Рис. 3.13. Конструкция коаксиального фильтра верхних частот для примера 3.3
Рис. 3.14. Расчетные характеристики фильтра верхних частот на элементах с сосредоточенными (—) и распределенными (---) параметрами к примеру 3.3
Дата добавления: 2015-02-03; просмотров: 1495;
