Расчет ступенчатых трансформаторов
На практике нередко требуется трансформировать одно сопротивление в другое. Например, к стандартному 50-омному генератору необходимо подключить элементы с очень высоким или очень низким входным сопротивлением, Эту проблему можно решить с помощью трансформатора сопротивления и получить такие значения волновых сопротивлений, при которых сравнительно просто реализуется линия передачи. Рассмотренные одиночные трансформирующие отрезки сохраняют требуемые свойства в весьма ограниченной рабочей полосе, т. е. они непригодны при широкополосной трансформации. Поэтому переходят к многоступенчатым трансформаторам. Уже двух- или трехступенчатые трансформаторы позволяют достигать рабочих полос до 150 %. Реальная полоса пропускания многоступенчатого трансформатора зависит от отношения R согласуемых сопротивлений, т. е. отношения сопротивлений, подключаемых к его входу и выходу.
Будем полагать, что согласуемые сопротивления чисто действительны. На практике редко применяют трансформаторы с числом четвертьволновых секций большим трех, т. к. на частотах до 10 ГГц полная длина трансформатора оказывается весьма значительной. Поэтому далее рассматриваются лишь двух- и трехступенчатые трансформаторы. Обозначения, используемые при проектировании ступенчатых трансформаторов сопротивления, указаны на рис. 3.20. Здесь Zви Zв3, Z3и Zв4 – согласуемые активные сопротивления (рис. 3.20, а, б).
Электрическая длина каждой секции трансформатора равна четверти длины волны в линии на центральной рабочей частоте. Если трансформатор конструируется из отрезков линии с дисперсией, в которой эффективная диэлектрическая проницаемость, а значит, и длина волны в линии зависят от частоты, то приближенно длину каждой секции можно определить по формуле
l ≈ λgв λgн/ 2 (λgв + λgн), (3.26)
где индексы "в" и "н" означают самую высокую и самую низкую частоты из рабочей полосы трансформатора. Независимо от наличия или отсутствия дисперсии на центральной частоте электрическая длина каждой секции должна быть 90˚. Относительная полоса пропускания B, которая фигурирует в дальнейшем обсуждении, вычисляется по формуле
B=2(λgн - λgв)/(λgн + λgв), (3.27)
Расчетные соотношения, приведенные в табл. 3.4 для трансформаторов с двумя и тремя секциями, являются строгими. Формулы для расчета двухступенчатого трансформатора с максимально плоской и чебышевской характеристиками, как видно в табл. 3.4, достаточно просты, и вычисления по ним можно проводить вручную, не прибегая к ЭВМ. Однако при проектировании трехступенчатого трансформатора ситуация сложнее, т. к. необходимо определять параметр V1 из нелинейного уравнения. Проще всего такое решение находится численно на ЭВМ методом итераций. Решив нелинейное урав-нение относительно V1, можно определить значения Zв1, Zв2, Zв3.
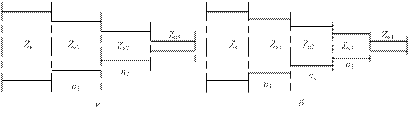
Рис. 3.20. Двухступенчатый (а) и трехступенчатый (б)трансформаторы сопротивления, состоящие из четвертьволновых отрезков
Поскольку при описанной выше методике синтеза пренебрегалось влияниемнеоднородностей, для реализации заданной характеристики трансформатора необходима некоторая экспериментальная доработка конструкции. Как показывает анализ, ширина полосы пропускания идеального многоступенчатого трансформатора сравнительно слабо зависит от числа секций в нем. Степень чувствительности зависит от отношения согласуемых сопротивлений. Кроме тoгo, из анализа следует, что увеличение числа секций в чебышевском трансформаторе обычно приводит к уменьшению амплитуды осцилляции в полосе пропускания. Качественно описанные выше эффекты иллюстрируются на рис. 3.21.
Максимальное значение KстU в полосе пропускания трансформатора зависит от отношения согласуемых сопротивлений и от требуемой относительной полосы пропускания. Например, для двухступенчатого чебышевского трансформатора при отношении согласуемых сопротивлений 3 : 1 и В = 0,2 максимальное значение KстU = 1,01, а при B = 1,0 возрастает до 1,47. Для трехступенчатого чебышевского трансформатора с тем же отношением согласуемых сопротивлений при В = 0,2 KстU ≈1,0, а при В = 1,01 KстU = 1,18. Из приведенных данных следует, что увеличение числа секций в трансформаторе при фиксированном отношении согласуемых сопротивлений и неизменной относительной полосе пропус-кания приводит к уменьшению максимального значения KстU.
Таблица 3.4
Формулы для расчета ступенчатых трансформаторов
| n = 2 n = 3 |
Максимально плоская характеристика
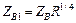 ; ; 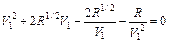 ; ;
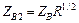 ; ; 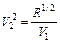 ; ;
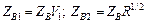 ; ;
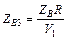 Чебышевская характеристика
Чебышевская характеристика
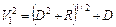 ; ; 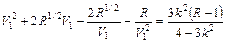 ; ;
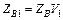 ; ; 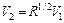 ; ;
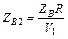 , , 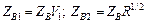 ; ;
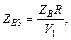
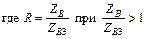 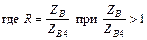
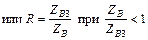 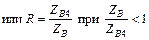
|
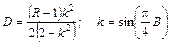
|
Пример 3.5. Спроектировать двухступенчатый трансформатор сопротивления, обеспечивающий согласование активных сопротивлений 50 и 100 Ом в относительной полосе частот 40 %. Трансформатор должен иметь чебышевскую характеристику.
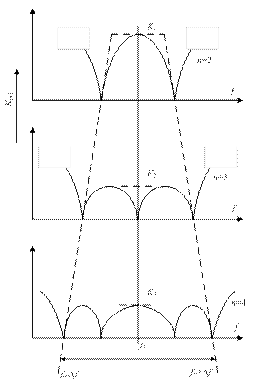 |
Рис. 3.21. Влияние чисел ступеней в чебышевском трансформаторе
на ширину полосы пропускания и амплитуду осцилляции
Решение
Определяем отношение сопротивлений: R = 100/50 = 2; относительная полоса пропускания В = 0,4, что соответствует 40 %. Тогда согласно табл. 3.4
k = sin(π∙0,4/4)=0,31,
т. е. 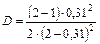 .
.
Далее находим
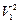 = (0,02522 + 2)1/2 + 0,0252 = 1,44,
= (0,02522 + 2)1/2 + 0,0252 = 1,44,
т. е. V1 = 1,2.
Определяем
Zв1 = 50∙1,2 = 60 Ом,
Zв1 = (50∙1,2)/1,2 = 83,3 Ом.
Расчет закончен.
Аналогично по формулам табл. 3.4 рассчитывается двухступенчатый трансформатор с максимально плоской характеристикой, В результате получаем Zв1 = 59,5 Ом; Zв2 = 84,1 Ом. Легко заметить малую разницу в значениях волновых сопротивлений секций двух рассчитанных трансформаторов, что обусловлено малым значением параметра D. По мере увеличения отношения согласуемых сопротивлений, особенно при R >> 1, результаты расчета трансформаторов с чебышевской и максимально плоской характеристиками все более различаются.
Дата добавления: 2015-02-03; просмотров: 2319;
