Оценка моделей с распределенными лагами с конечным числом лагов.
В эконометрике, модель с распределённым лагом - это модель временного ряда, в которой в уравнение регрессии включено как текущее значение объясняющей переменной, так и значения этой переменной в предыдущих периодах. Модель с конечным числом лагов:
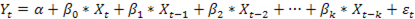 ; или
; или
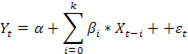
k – максимальная величина лага.
Для оценки данной спецификации используется метод замены переменных:
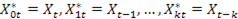
Спецификация модели:
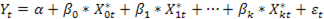
Однако мы теряем первые k наблюдений, t=k+1, …, n
73. Оценка моделей с распределенными лагами с бесконечным числом лагов: метод геометрической прогрессии.
В эконометрике, модель с распределённым лагом - это модель временного ряда, в которой в уравнение регрессии включено как текущее значение объясняющей переменной, так и значения этой переменной в предыдущих периодах. Модель с бесконечным числом лагов:
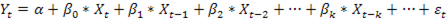 ;
;
Модели, включающие в качестве лаговых переменных (объясняющих) зависимые переменные, называются авторегрессионными:
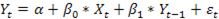 .
.
Метод геометрической прогрессии:
Предполагается, что коэффициенты 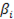 при лаговых значениях объясняющей переменной убывают в геометрической прогрессии:
при лаговых значениях объясняющей переменной убывают в геометрической прогрессии:
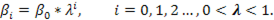
𝛌 – характеристика скорости убывания коэффициентов с увеличением лага.
Такое предположение достаточно логично, если считать, что влияние прошлых значений объясняющих переменных на текущее значение зависимой переменной будет тем меньше, чем дальше по времени эти показатели имели место.
Тогда модель геометрической прогрессии:
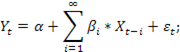
Спецификация модели с геометрически распределёнными лагами:
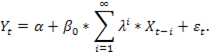
Параметры данного уравнения 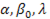 можно определять различными способами. Например, параметру
можно определять различными способами. Например, параметру 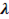 присваиваются последовательно все значения из интервала (0,1) с произвольным фиксированным шагом (например, 0,01; 0,001; 0,0001). Для каждого
присваиваются последовательно все значения из интервала (0,1) с произвольным фиксированным шагом (например, 0,01; 0,001; 0,0001). Для каждого 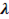 рассчитывается:
рассчитывается:
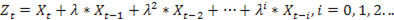
Значение i определяется из условия, что при дальнейшем добавлении лаговых значений Х величина изменения 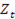 менее любого, ранее заданного числа.
менее любого, ранее заданного числа.
Далее оценивается уравнение регрессии:
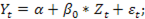
Из всех возможных значений 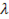 выбирается то, при котором коэффициент детерминации
выбирается то, при котором коэффициент детерминации 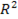 для уравнения регрессии будет наибольшим. Найденные при этом параметры
для уравнения регрессии будет наибольшим. Найденные при этом параметры 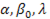 подставляются в
подставляются в
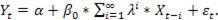 Возможности современных компьютеров позволяют произвести указанные расчёты за приемлемое время.
Возможности современных компьютеров позволяют произвести указанные расчёты за приемлемое время.
74. Оценка моделей с распределенными лагами с бесконечным числом лагов: метод Койка.
В эконометрике, модель с распределённым лагом - это модель временного ряда, в которой в уравнение регрессии включено как текущее значение объясняющей переменной, так и значения этой переменной в предыдущих периодах. Модель с бесконечным числом лагов:
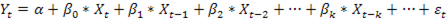 ;
;
Модели, включающие в качестве лаговых переменных (объясняющих) зависимые переменные, называются авторегрессионными:
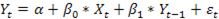 .
.
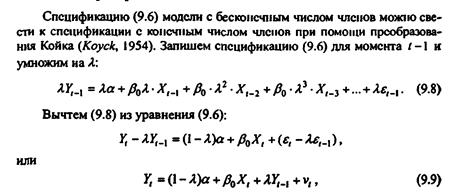

75. Проблемы оценки параметров регрессионных моделей с распределёнными лагами методом Койка
Спецификация включает стохастический регрессор, коррелирующий со случайным возмущением. Т.е. среди регрессоров появляется лаговая переменная, которая представляет собой стохастический регрессор, что нарушает одну из предпосылок Гаусса-Маркова для классической регрессионной модели, данная случайная переменная коррелирует со случайным возмущением.
Случайные возмущения исходной модели с распределенными лагами не коррелированы, случайные возмущения авторегрессионной модели автокоррелированы. Для случайных возмущений исходной модели справедлива предпосылка о некоррелированности, а для случайного возмущения преобразованной модели имеет место автокорреляция.
76. Оценка моделей с распределенными лагами: метод Алмон.
В эконометрике, модель с распределённым лагом - это модель временного ряда, в которой в уравнение регрессии включено как текущее значение объясняющей переменной, так и значения этой переменной в предыдущих периодах.
В общем случае, модель имеет вид:
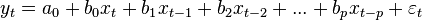
или
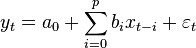
Встречаются ситуации, когда значения лаговой объясняющей переменной за 3-4 периода от момента наблюдения оказывают на зависимую переменную большее влияние, чем текущее или предшествующее ему значение объясняющей переменной (b3, b4 > b0, b1).
Pacnpeделённые лаги Алмон позволяют моделировать такие изменения.
В основе модели Алмон лежит предположение, что «веса» коэффициентов bi в модели 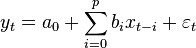 могут выражаться полиномами определенной степени от величины лага:
могут выражаться полиномами определенной степени от величины лага:
bi = a0 + a1*i + a2*i2 + …+ am*im.
Пример: Это может быть квадратичная зависимость:
bi = a0 + a1*i + a2*i2.
Или полином третьей степени:
bi = a0 + a1*i + a2*i2 + a3*i3
Для применения схемы Алмон необходимо вначале определиться с количеством лагов k. Обычно это количество находится подбором, начиная с «разумного» максимального, постепенно его уменьшая.
Для примера, пусть k=2 и bi описывается квадратичным полиномом, тогда:
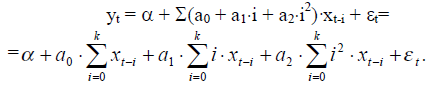
Сделаем замену переменных:
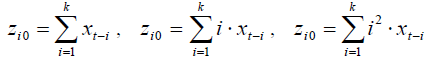
После чего имеем:
Yt = a + a0×zt0 + a1×zt1 + a2×zt2 + et.
Получили линейную модель, Значения a, a0, a1, a2 могут быть определены по МНК.
Дата добавления: 2015-01-10; просмотров: 6504;
