Проблема идентификации системы одновременных уравнений СОУ.

Запишем структурную форму эконометрической модели в матричном виде:

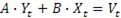, (1.1), где 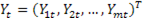– вектор-столбец значений эндогенных переменных, определяемых внутри модели (m – число эндогенных переменных в системе);

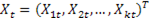– вектор-столбец значений предопределенных переменных, которые могут включать как экзогенные переменных (внешние по отношению к системе), так и лаговые значение эндогенных переменных (k – число предопределенных переменных в системе);

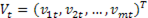- вектор-столбец случайных возмущений; t – номер (момент) наблюдения;

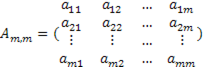
· Матрица коэффициентов перед вектором эндогенных переменных модели;

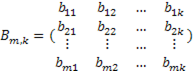
- Матрица коэффициентов перед вектором предопределенных переменных модели. Одно из основных требований к предопределенным переменным – некоррелированность со случайными возмущениями в каждом наблюдении t.
Предполагая что матрица А невырождена, умножив обе части равенства (1.1) на , получим приведенную форму модели:

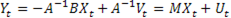, (1.2), где 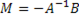(1.3) – матрица коэффициентов приведенной формы, 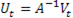(1.4) – вектор случайных возмущений приведенной формы.

Как следует из (1.3), структурные коэффициенты А и В связаны с приведенными коэффициентами модели соотношением: 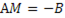(1.5).

В общем случае, как было показано выше, эндогенные переменные одного уравнения структурной формы могут быть регрессорами в других уравнениях, что приводит к их коррелированности со случайными возмущениями, поэтому применение к какому-либо из уравнений МНК дает смещенные и несостоятельные оценки. Коэффициенты приведенной формы могут быть состоятельно оценены МНК, поскольку регрессоры приведенной формы некоррелированы со структурными возмущениями 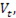и следовательно (см.(1.4)), с приведенными возмущениями 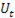. Т.о., задача состоит в оценке структурных коэффициентов по приведенным. Рассчитаем количество исходных данных, которые могут быть использованы при определении структурных параметров:

· mk – элементов матрицы М приведенных коэффициентов;

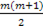· – элементов атоковариационной матрицы вектора возмущений .

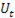В структурной форме неизвестными являются:

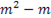· – число элементов матрицы А (с учетом нормализации);

· mk – элементов матрицы В;

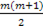· – элементов атоковариационной матрицы вектора возмущений .

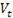Т.о., неизвестных структурных коэффициентов больше, чем оцененных приведенных на величину 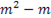, и, следовательно, в общем случае система одновременных уравнений неидентифицируема.

Однако при наличии априорных ограничений на структурные коэффициенты некоторые структурные уравнения могут быть идентифицированы, поэтому в дальнейшем будет рассматриваться задача идентификации отдельного уравнения. В качестве ограничений на структурные коэффициенты обычно используются следующие простейшие:

· Часть структурных коэффициентов равна нулю, т.е. между экономическими переменными, входящими в систему, в данном уравнении нет связи;

· Часть структурных коэффициентов равна единице (в случае тождества, или условия нормализации).

Если таких ограничений недостаточно для однозначного определения структурных коэффициентов через приведенные, то говорят, что уравнение неидентифицируемо.

80. Идентификация отдельных уравнений системы одновременных уравнений: порядковое условие.

Необходимое условие идентификации уравнения:

k-p 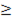q-1, где

k – число предопределенных переменных в системе;

p – число предопределенных переменных в уравнении;

q – число эндогенных переменных в уравнении.