Ранговое условие идентификации.

i-е уравнение модели идентифицируемо тогда и только тогда, когда справедливо равенство:

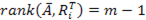(с учетом нормализации).

Обозначение:

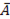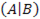= – расширенная матрица структурной формы.

82. Косвенный метод наименьших квадратов: алгоритм метода; условия применения

Косвенный метод наименьших квадратов используется в случае точно идентифицируемой структурной модели. Процедура применения косвенного метода предполагает выполнение следующих этапов работы:

1. структурная модель преобразовывается в приведенную форму модели;

то есть, например:

для модели

y_1t = a₁₂ * y_2t + b₁₁ * x_1t + v_1t

y_2t = a₂₁ * y_1t + b₂₂ * x_2t + v_2t

приведенная форма будет иметь вид:

y_1t = m₁₁ * x_1t + m₁₂ * x_2t + u_1t

y_2t = m₂₁ * x_1t + m₂₂ * x_2t + u_2t.

2. для каждого уравнении приведенной формы модели обычным методом наименьших квадратов оцениваются приведенные коэффициенты (δ_ij);

3.коэффициенты приведенной формы модели трансформируются в параметры структурной модели.

То есть, например:

для оценки структурных параметров по приведенным воспользуемся равенством AM = -B , переписанное в виде AM + B = 0, или через расширенную матрицу структурной формы А̄ = (А|B) :

А̄ * ( ) = 0,где I – единичная матрица k x k. Для оценки коффициентов i-й строки матрицы А̄, помимо приведенного выше соотношения, учтем априорные ограничения: условие нормализации и равенство нулю некоторых структурных коэффициентов. Получается, что вектор коэффициентов i-й строки матрицы удовлетворяет следующей системе уравнений:

,

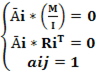можно показать, что если i-е уравнение идентифицируемо и выполнено условие нормализации, то система имеет единственное решение. Если значение элементов матрицы приведенной системы М известны, то в системе (1.2) используются их МНК-оценки.

Для оценок структурных параметров в косвенном методе наименьших квадратов используются МНК – оценки параметров приведенных уравнений.

Косвенный метод наименьших квадратов предназначен для оценивания структурных параметров отдельного уравнения системы и может дать результат (без сочетания с другими методами, например, с двухшаговым методом наименьших квадратов) только в применении к точно идентифицируемому уравнению.

83. Двухшаговый метод наименьших квадратов (ДМНК): алгоритм метода; условия применения.

В зависимости от того, является уравнение системы идентифицируемым или сверхидентифицируемым, используются различные методы оценки его структурных параметров. Двухшаговый метод наименьших квадратов позволяет построить оценки параметров как точно, так и сверхидентифицируемых уравнений.

Объясним метод ДМНК на примере уравнения

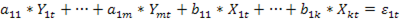
системы 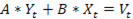. Введем обозначения:

1. 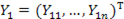- вектор наблюдений эндогенной переменной, для которой выполняется условие нормализации.

2. 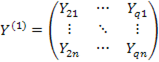-матрица наблюдений остальных эндогенных переменных, включенных в первое уравнение.

3. 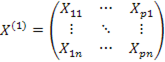-матрица наблюдений предопределенных переменных, включенных в первое уравнение

4. 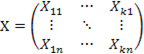-матрица наблюдений предопределенных переменных, включенных в систему

5. 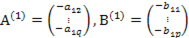-структурные параметры уравнения

6. 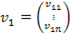-вектор случайных возмущений первого уравнения.

7. 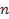– объем выборки

8. 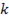– число предопределенных переменных в системе

Тогда уравнение примет вид: 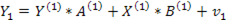, а спецификацию можно представить в форме: 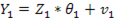, где:

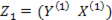· - блочная матрица

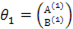· - блочный столбец

Поскольку элементы матрицы 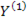коррелированы с элементами вектора 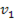, применение МНК невозможно (приводит к смещенным и несостоятельным оценкам). В связи с этим, следует использовать ДМНК. Алгоритм использования ДМНК:

1. Первый шаг

a. Проводится регрессия каждого столбца матрицы 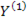спецификации на все предопределенные переменные модели, т.е. рассматривается регрессия 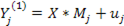, где 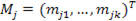- вектор - столбец приведенных параметров. МНК оценки вектора M_j определяются по формуле: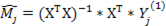

b. По оцененной модели вычисляется оценка
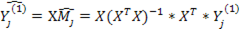и формируется матрица оценок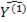

2. Строятся МНК-оценки структурных параметров 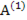и 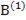в регрессии:
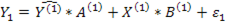, или аналогично 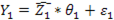, где

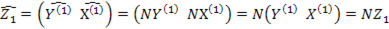
МНК оценка параметров регрессионной модели имеет вид:

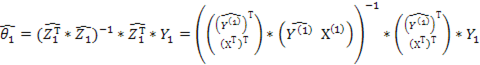. Далее, вектор оценок параметров спецификации можно представить в виде:

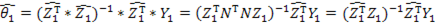, с учетом идемпотентности матрицы N.

В случае, если для уравнения выполнено ранговое условие идентификации и порядковое условие со знаком равенства (точно идентифицируемо), то оценка ДМНК совпадает с оценкой КМНК.