Шаталова Галина 9 страница
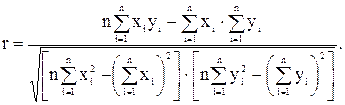 (5.8)
(5.8)
Чем ближе r к 1, тем ближе зависимость у=f(х) к линейной. Если |r| < 0,5, зависимость следует признать нелинейной. В зависимости от вида экспериментальной кривой ее аппроксимируют различными функциями (рис. 5.4). Для определения коэффициентов эмпирических формул можно использовать метод выравнивания, при котором переменные х и у заменяются другими, между которыми существует линейная зависимость. Например, если искомая зависимость имеет вид y=a·xC, то логарифмируя правую и левую части, получим ln y=ln a+Cln x или Y=А+CX. Теперь коэффициенты А и С могут быть найдены методом наименьших квадратов по формуле (1), в которую вместо 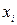 и
и 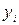 подставляют
подставляют 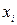 =ln
=ln 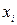 и
и 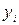 =ln
=ln 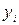 . Коэффициент С определяется сразу, а для определения а проводят потенцирование а = еA. Приемы замены для различных функций указаны в справочниках. Для оценки точности описания экспериментальных данных может быть использован коэффициент корреляции, рассчитанный по формуле (5.8) с подстановкой Xi и Yi. Чем ближе |r| к 1, тем лучше описываются экспериментальные данные выбранным видом зависимости.
. Коэффициент С определяется сразу, а для определения а проводят потенцирование а = еA. Приемы замены для различных функций указаны в справочниках. Для оценки точности описания экспериментальных данных может быть использован коэффициент корреляции, рассчитанный по формуле (5.8) с подстановкой Xi и Yi. Чем ближе |r| к 1, тем лучше описываются экспериментальные данные выбранным видом зависимости.
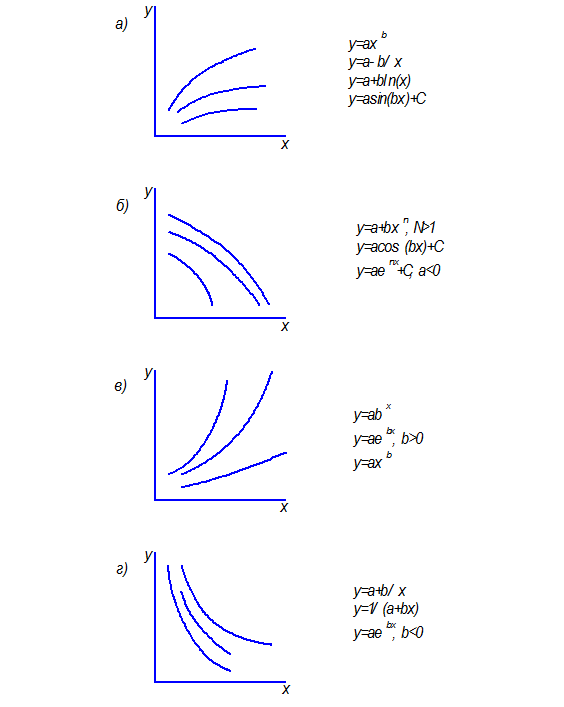
Рис. 5.4. Типовые графики и некоторые аппроксимирующие их выражения
Кроме метода наименьших квадратов могут использоваться и другие, например, метод избранных точек. В этом случае на плавной кривой намечается столько точек, сколько неизвестных коэффициентов в выбранной формуле (рис. 5.5). Их координаты подставляются в формулу, и решается полученная система уравнений. Например, в рассматриваемом случае
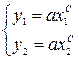 или
или 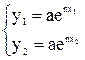 ,
,
где (x1,y2) и (x1,y2) – координаты первой и второй избранных точек.
Для подбора эмпирических формул могут также использоваться неравномерные координатные сетки и эталонные кривые. В последнее время при подборе эмпирических формул все чаще применяются ЭВМ (расчет коэффициентов при этом обычно основан на методе наименьших квадратов и замене переменных).
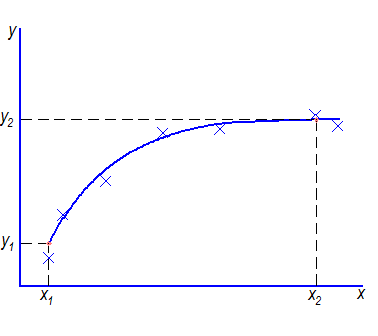
Рис. 5.5. Метод избранных точек: x-экспериментальные точки; •-избранные точки
3. МАТЕРИАЛЫ И ОБОРУДОВАНИЕ
Оборудование
1. Персональный компьютер.
4. ПРОГРАММА РАБОТЫ
1. Получить задание на работу (набор экспериментальных данных), построить график y=f(x) и выбрать вид функции.
2. Подобрать эмпирическую формулу, описывающую представленные данные, одним из известных способов без использования ЭВМ (кроме микрокалькулятора).
3. Продолжить работу в режиме диалога с ЭВМ: подобрать несколько вариантов эмпирической формулы и выбрать из них наиболее подходящий.
5. СОДЕРЖАНИЕ ОТЧЕТА
1. Цель работы.
2. Программа работы.
3. Индивидуальное задание.
4. Первоначально подобранная эмпирическая формула с описанием этапов подбора.
5. Варианты эмпирических формул, подобранные с помощью ЭВМ, построенные по формулам графики с указанием заданных экспериментальных точек, коэффициенты корреляции различных зависимостей.
6. Выводы, приводящие обоснование выбранного варианта эмпирической формулы.
6. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Какие виды формул Вы знаете?
2. Что такое метод наименьших квадратов?
3. Как подобрать эмпирическую формулу по имеющимся экспериментальным данным?
4. Что такое коэффициент корреляции?
5. Какие виды зависимостей или функций наиболее часто используются при подборе эмпирических формул?
Лабораторная работа № 4
ПЛАНИРОВАНИЕ И ОБРАБОТКА РЕЗУЛЬТАТОВ
МНОГОФАКТОРНЫХ ЭКСПЕРИМЕНТОВ
1. ЦЕЛЬ РАБОТЫ
Изучить основные понятия и приобрести практические навыки математического планирования и обработки результатов много факторных экспериментов.
2. ОСНОВНЫЕ ЭТАПЫ ФАКТОРНОГО ПЛАНИРОВАНИЯ
ЭКСПЕРИМЕНТА
Технологические процессы, в частности сварка и пайка, характеризуются одновременным воздействием на изделие многих технологических факторов. Применение вместо классического метода математического планирования эксперимента позволяет при исследовании технологических процессов сократить время и повысить точность результатов, оптимизировать технологические режимы, а также создавать системы автоматического управления технологическими процессами.
Математическое планирование эксперимента – это процедура выбора числа и условий постановки опытов, необходимых и достаточных для решения данной задачи с требуемой точностью, методов математической обработки их результатов и принятия решений.
Основными этапами наиболее распространенного варианта факторного планирования эксперимента являются следующие.
Выбор выходного параметра и факторов планирования
Количество параметров, характеризующих объект исследования, теоретически бесконечно. От правильного выбора выходного параметра (а при поиске наилучших условий функционирования объекта – критерия оптимизации) и факторов, изменяемых при проведении эксперимента (факторов планирования), зависит успех исследования. Выбор выходного параметра и факторов планирования производится на основании сведений о изучаемом и родственных объектах (так называемой априорной информации).
Выбранный выходной параметр обязан отвечать условию однозначности, т.е. заданному выбору значений факторов должно соответствовать одно значение выходного параметра (с учетом погрешности эксперимента). Критерий оптимизации должен эффективно оценивать функционирование всего процесса. Целесообразно также, чтобы критерий имел физический смысл, был простым, легко вычисляемым и позволял осуществлять всевозможные комбинации факторов. Качество процесса часто характеризуется несколькими параметрами. Однако движение к оптимуму упрощается, если выбран только один параметр оптимизации (остальные показатели в этом случае могут служить ограничениями).
Факторы планирования должны быть управляемыми, не взаимосвязанными, количественными. Погрешность измерения фактора должна быть в 3-5 раз меньше погрешности выходного параметра. Следует стремиться к учету всех факторов, существенно влияющих на выходной параметр. Однако с увеличением количества факторов либо возрастает количество опытов, либо уменьшается точность математической модели.
Выбор среднего уровня фактора 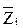
Обычно в качестве среднего уровня принимают значение, соответствующее наилучшему с точки зрения предшествующего знания об объекте значению выходного параметра. Если это значение близко к границе возможной области изменения фактора, средний уровень выбирают с некоторым сдвигом от наилучших условий.
Выбор интервалов варьирования hi
На первом этапе эксперимента обычно получают линейную модель объекта. Для построения такой модели факторы при проведении опытов должны принимать только два значения – верхний и нижний уровни. Интервал варьирования – разность между значениями фактора на среднем и верхнем (нижнем) уровнях.
Интервал варьирования должен быть больше ошибки определения уровня фактора, но уровни фактора не должны выходить за границы области исследования. Значение факторов в эксперименте:
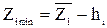 ;
;
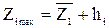 .
.
Переход от натуральных переменных Zi к условным переменным Xi
Для упрощения записи условий эксперимента и расчетов при обработке экспериментальных данных натуральные переменные заменяют кодированными (условными). Для количественных факторов замена проводится по формулам
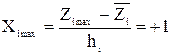 ,
,
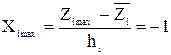 .
.
Составление матрицы планирования
Матрица планирования - это таблица, описывающая условия проведения опытов, в которой строки соответствуют различным опытам, а столбцы - значениям факторов. Уровни факторов в матрице (+1 или –1) часто обозначают просто знаками (+ или – ). При полном факторном эксперименте реализуются все возможные сочетания уровней факторов (табл. 5.2, 5.3).
Таблица 5.2
Два фактора. Полный факторный эксперимент 22
| Номер опыта | Значения факторов | |
| X1 | X2 | |
| – | – | |
| + | – | |
| – | + | |
| + | + |
Таблица 5.3
Три фактора. Полный факторный эксперимент 23
| Номер опыта | Значение факторов | ||
| X1 | X2 | X3 | |
| – | – | + | |
| – | + | – | |
| + | – | – | |
| + | + | + | |
| – | – | – | |
| – | + | + | |
| + | – | + | |
| + | + | – |
Для сокращения количества опытов обычно предпочитают дробный факторный эксперимент, т.е. не полный перебор всех возможных сочетаний уровней факторов, а строго определенное их сочетание, позволяющее рассчитать коэффициенты математической модели. Однако с повышением дробности матрицы уменьшается точность расчета коэффициентов модели и возможность установления совместного действия нескольких факторов. Для составления матрицы планирования существуют специальные правила. В табл. 5.4 – 5.7 приведены возможные варианты матриц планирования для 3-6 факторов и числа опытов не более 6.
Таблица 5.4
Три фактора. Дробный факторный эксперимент 23-1
| Номер опыта | Значение факторов | ||
| X1 | X2 | X3 | |
| – | – | – | |
| + | + | – | |
| – | + | + | |
| + | – | + |
Таблица 5.5
Четыре фактора. Дробный факторный эксперимент 24-1
| Номер опыта | Значение факторов | |||
| X1 | X2 | X3 | X4 | |
| – | – | – | – | |
| + | + | – | – | |
| + | – | + | – | |
| + | – | – | + | |
| – | + | + | – | |
| – | + | – | + | |
| – | – | + | + | |
| + | + | + | + |
Таблица 5.6
Пять факторов. Дробный факторный эксперимент 25-2
| Номер опыта | Значения факторов | ||||
| X1 | X2 | X3 | X4 | X5 | |
| – | – | – | – | – | |
| + | + | – | – | – | |
| – | – | + | + | – | |
| + | – | + | – | + | |
| – | + | + | – | + | |
| + | – | – | + | + | |
| – | + | – | + | + | |
| + | + | + | + | – |
Таблица 5.7
Шесть факторов. Дробный факторный эксперимент 26-3
| Номер опыта | Значения факторов | |||||
| X1 | X2 | X3 | X4 | X5 | X6 | |
| – | – | – | – | – | – | |
| + | – | + | – | – | + | |
| + | – | – | + | + | – | |
| – | + | + | – | + | – | |
| – | + | – | + | – | + | |
| + | + | + | + | – | – | |
| + | + | – | – | + | + | |
| – | – | + | + | + | + |
Одновременно с матрицей значений условных переменных составляется и матрица значений натуральных переменных в опытах.
Проведение эксперимента
Опыты по матрице планирования необходимо выполнять в случайном порядке, каждый опыт в одних и тех же условиях повторять несколько раз.
Проверка воспроизводимости опытов
По результатам повторных опытов вычисляют в каждой строке матрицы:
– среднее арифметическое
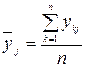 , (5.9)
, (5.9)
где n – количество опытов, выполненных при одинаковых условиях
(j строка);
ykj – значение выходного параметра в k-ом опыте j-строка;
– дисперсию:
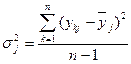 . (5.10)
. (5.10)
Проверяют однородность дисперсий. Если число повторных опытов во всех строках матрицы одинаково, проверка производится по критерию Кохрена:
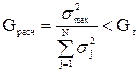 , (5.11)
, (5.11)
где Gрасч – рассчитанное значение критерия Кохрена;
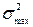 – максимальная из всех построчных дисперсий;
– максимальная из всех построчных дисперсий;
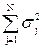 – сумма построчных дисперсий во всех N строках матрицы;
– сумма построчных дисперсий во всех N строках матрицы;
Gт – табличное значение критерия Кохрена (табл. 5.8).
Таблица 5.8
Значение критерия Кохрена для различного числа опытов
при доверительной вероятности 0,95
| Число строк матрицы планирования | Число опытов в каждой строке матрицы | |||
| 0,907 | 0,768 | 0,684 | 0,629 | |
| 0,680 | 0,516 | 0,438 | 0,391 |
Если расчетное значение критерия Кохрена больше допустимого, математическую модель строить нельзя. Необходимо повторить опыты данной строки либо перестроить схему эксперимента с целью повышения его точности.
Для дальнейших расчетов определяют дисперсию воспроизводимости:
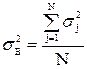 . (5.12)
. (5.12)
Расчет коэффициентов уравнения регрессии
Вследствие воздействия случайных факторов результаты опытов, проведенных в одних и тех же условиях (с точки зрения исследователя), будут отличаться друг от друга. Поэтому после их обработки можно указать только наиболее вероятное значение выходного параметра при данных значениях факторов. В таких случаях связь между выходными параметрами и факторами называют корреляционной, а описывающее ее уравнение - уравнением регрессии. При построении линейной модели объекта уравнение регрессии имеет вид:
y=b0+b1x1+b2x2+…+bixi+…bm-1·xm-1 (5.13)
Коэффициенты уравнения регрессии рассчитывают по формуле:
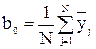 ;
; 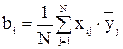 , (5.14)
, (5.14)
где xij – значение i-того фактора в j-й строке матрицы планирования.
Оценка значимости коэффициентов уравнения регрессии
Оценка значимости коэффициентов проводится для отбрасывания членов уравнения (5.13), незначительно влияющих на выходной параметр. В результате упрощаются расчеты.
Определяется доверительный интервал
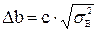 , (5.15)
, (5.15)
где 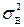 - рассчитанная по формуле (5.12) дисперсия воспроизводимости;
- рассчитанная по формуле (5.12) дисперсия воспроизводимости;
с – постоянная, зависящая от числа строк матриц и количества опытов в каждой строке (табл. 5.9).
Таблица 5.9
Коэффициент С для расчета доверительного интервала
| Количество строк в матрице | Количество опытов, проведенных в условиях каждой строки | |||
| 1,15 | 1,06 | 1,03 | 1,02 | |
| 0,81 | 0,75 | 0,73 | 0,72 |
Значимость коэффициентов уравнения регрессии определяется из условия |bi|>Δb. Если абсолютная величина коэффициента регрессии bi меньше доверительного интервала, фактором xi можно пренебречь.
Проверка адекватности уравнения регрессии
Определяется дисперсия адекватности:
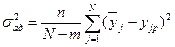 . (5.16)
. (5.16)
где n – число параллельных опытов;
N – количество строк матрицы планирования;
m – количество коэффициентов уравнения (5.13), считая b0;
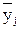 и yjр – среднее экспериментальное и рассчитанное по уравнению (5.13) значение выходного параметра для условий j-й строки матрицы.
и yjр – среднее экспериментальное и рассчитанное по уравнению (5.13) значение выходного параметра для условий j-й строки матрицы.
Определяют критерий Фишера:
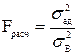 .
.
Уравнение (5.13) считается адекватным, если Fрасч<Fтабл (табл. 5.10).
Таблица 5.10
Значение критерия Фишера при доверительной вероятности 0,95
| Число степеней свободы дисперсии воспроизводимости fВ=N(n-1) | Число степеней свободы дисперсии адекватности fад=N-m | ||||
| 7,7 | 6,9 | 6,6 | 6,4 | 6,3 | |
| 5,3 | 4,5 | 4,1 | 3,8 | 3,7 | |
| 4,8 | 3,9 | 3,5 | 3,3 | 3,1 | |
| 4,5 | 3,6 | 3,2 | 2,9 | 2,8 | |
| 4,3 | 3,4 | 3,0 | 2,8 | 2,6 | |
| 4,2 | 3,3 | 2,9 | 2,7 | 2,5 |
Если уравнение неадекватно, необходимо перейти к неполной или полной квадратичной модели.
Переход к неполной квадратичной модели, в которой к правой части уравнения (5.13) добавляются слагаемые вида bil·xi·xl (причем i≠l), может быть осуществлен без проведения дополнительных опытов.
Коэффициенты, учитывающие одновременное изменение двух факторов, рассчитываются по формуле:
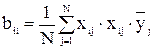 .
.
Однако при этом эффекты взаимодействия различных факторов могут накладываться друг на друга. Например, при проведении опытов по матрице (табл. 5.5) коэффициенты b12 и b34 равны. При получении значимых коэффициентов взаимодействия можно попытаться отнести их к тому или иному взаимодействию, исходя из физического смысла, а также из сравнения коэффициентов, полученных для каждого из факторов.
Для перехода к полной квадратичной модели, включающей слагаемые вида 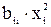 , необходимо проведение дополнительных опытов.
, необходимо проведение дополнительных опытов.
Переход к натуральным показателям
Если уравнение адекватно, осуществляют переход от условных переменных к натуральным. Для этого уравнение (5) подставляют 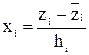 и получают уравнение вида:
и получают уравнение вида:
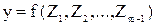 ,
,
которым удобнее пользоваться для расчета выходного параметра внутри исследованной области. Решение задачи интерполяции на этом заканчивается.
Расчет крутого восхождения
Если решается задача оптимизации и требуемые значения выходного параметра не достигнуты, после получения адекватного уравнения регрессии обычно принимают решение использовать метод крутого восхождения. Изменяя независимые переменные пропорционально величинам коэффициентов регрессии, условия процесса приближают к оптимальным по самому крутому пути. Восхождение начинают из нулевого уровня.
Один из факторов (обычно оказывающий наибольшее влияние на выходной параметр) принимают за базовый. Выбирают шаг движения по базовому фактору:
ΔZб=γ·hб,
где γ – коэффициент, принимаемый обычно в пределах 0,3…0,9;
hб – интервал варьирования базового фактора.
Затем рассчитывают шаги движения по факторам, пропорционально произведениям коэффициентов регрессии на интервалы варьирования:
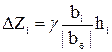 .
.
Факторы планирования в опытах принимают значения
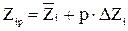 ,
,
где p – номер шага крутого восхождения.
Проведение опытов крутого восхождения
Крутое восхождение считается эффективным, если хотя бы в одном опыте достигнут результат, лучший по сравнению с наилучшим результатом в опытах по матрице планирования. Крутое восхождение прекращают, если уровни факторов или выходного параметра вышли за допустимые пределы либо достигнут экстремум параметра оптимизации.
3. МАТЕРИАЛЫ И ОБОРУДОВАНИЕ
Оборудование
1. Персональный компьютер.
4. ПРОГРАММА РАБОТЫ
1. Изучить методические указания.
2. Получить задание на работу.
3. Выбрать выходной параметр (критерий оптимизации) факторы планирования, составить матрицу планирования.
4. Ввести запрашиваемые данные и выполнить все необходимые этапы планирования эксперимента на персональном компьютере.
5. Сформулировать выводы по работе.
5. СОДЕРЖАНИЕ ОТЧЕТА
1. Цель работы.
2. Программа работы.
3. Индивидуальное задание.
4. Вариант классического плана эксперимента.
5. Обоснование и расчеты по планированию и обработке результатов эксперимента.
6. Выводы.
6. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Преимущества метода математического планирования эксперимента по сравнению с классическим.
2. Как производится выбор интервалов варьирования?
3. Что такое дробный факторный эксперимент?
4. Для чего производится оценка значимости коэффициентов уравнения регрессии?
5. В каких случаях используется метод крутого восхождения?
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Основная литература
1. Справочник по пайке / под ред. И.Е. Петрунина. – 3-е изд., перераб. и доп. – М. : Машиностроение, 2003. – 480 с.
Дополнительная литература
1. Кане, М.М. Основы научных исследований в технологии машиностроения / М.М. Кане. – М. : Высш. шк., 1987. – 231 с.
2. Основы научных исследований / под ред. В.И. Крутова, В.В. Попова. – М. : Высш. шк., 1989. – 400 с.
Шаталова Галина
ЗДОРОВЬЕ ЧЕЛОВЕКА:
Дата добавления: 2015-01-29; просмотров: 1290;
