Исследование плоского напряженного состояния

Плоское напряженное состояние возникает в точке, если все напряжения на одной из координатных осей равны нулю.

.

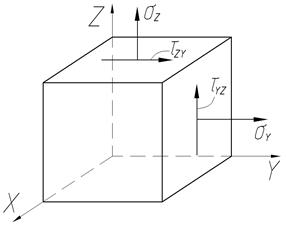
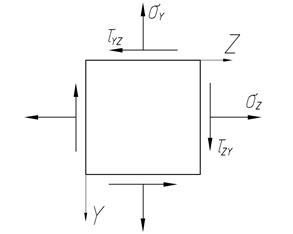
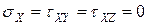В этом случае схему нагружения малого объема можно представить плоской.

Эта плоская область по-прежнему является точкой.

Кубическое уравнение 7.5 принимает вид квадратного

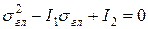(7.6)

Инварианты для уравнения 7.6 принимают вид

,

,

.

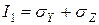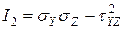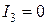Решая квадратное уравнение 7.6, получим два действительных корня, которые будут главными напряжениями. Но так как главных напряжений три, то для плоского состояния одно из них всегда будет равно нулю.

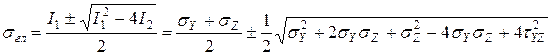
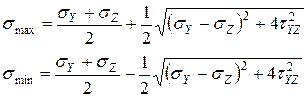(7.7)

Индексы выбираются по правилу 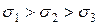. Например, получены корни 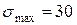, , 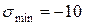тогда , , .

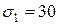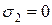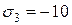Однако, зная значения главных напряжений, мы не можем установить ориентацию главной площадки по отношению к тем, которые заданы.

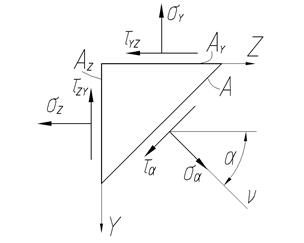
Эту задачу можно решить, если исследовать напряжения на площадке общего положения.

Составим уравнения равновесия сил в проекциях на ось .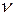

; .

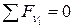
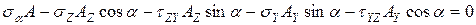
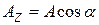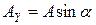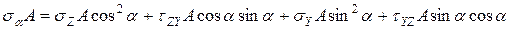
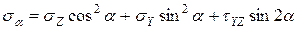(7.8)

Аналогично, составив уравнение равновесия, получим .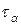

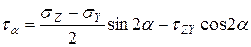(7.9)

Вычисляя значения 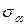и 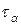необходимо использовать следующее правило знаков: нормальные напряжения считаются положительными, если они действуют от площадки, касательные напряжения считаются положительными, если они стремятся повернуть свою площадку по часовой стрелке.

Так как на главной площадке касательное напряжение равно нулю 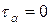, то из формулы 7.9 можно определить ее ориентацию

; ; ;

.

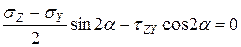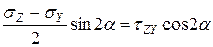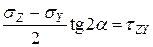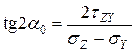Угол 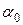– то угол, на который откланяется главная площадка от заданной.

======================= 10 ========================