Кубическое уравнение для определения главных напряжений

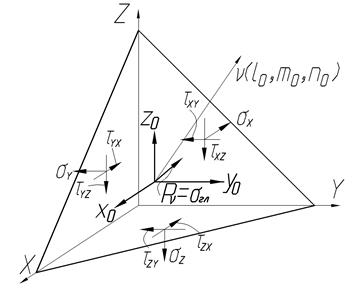
Рассмотрим тетраэдр, на площадку которого действует напряжение .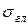

Направляющие косинусы будут , , .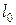

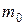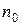Проекции напряжения 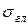запишутся в виде

, , .

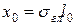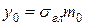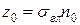Из выражений 7.3 получим запись этих проекций

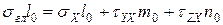
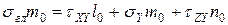
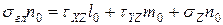
Из полученных выражений составим систему однородных уравнений

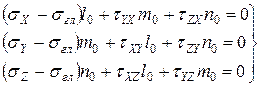(7.4)

7.4 это система однородных уравнений направляющих косинусов. Направляющие косинусы взаимосвязаны. Так как они ортогональны, то сумма их квадратов равна единице

.

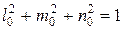Направляющие косинусы также не равны нулю. Поэтому должен равняться нулю определитель, полученный из уравнений 7.4

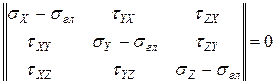
Определитель раскрывается методом Краммера, в результате чего получается кубическое уравнение

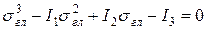, (7.5)

где 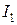, , 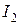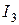– коэффициенты кубического уравнения.

Каждому нагруженному малому объему соответствует реальная физическая задача, поэтому, даже без строгого математического доказательства, можно указать на тот факт, что это уравнение имеет три корня ( 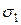, , 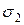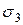), которые являются действительными числами. Это главные напряжения и они подчиняются правилу .

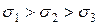Главные напряжения важны в общей оценке прочности, как отдельного стержня, так и трехмерно нагруженного тела.

Инварианты тензора напряжений

Коэффициенты из кубического уравнения 7.5 определяются по следующим выражениям:

,

,

.

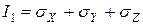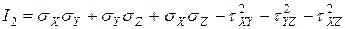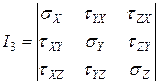
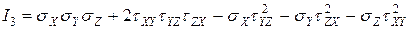Эти коэффициенты называются инвариантами преобразования системы координат, т.е. это величины, которые не изменяются при преобразовании системы координат. Например, длина любого отрезка в любой системе координат величина постоянная, в то время, как точки начала и конца его зависят от выбранной системы координат.