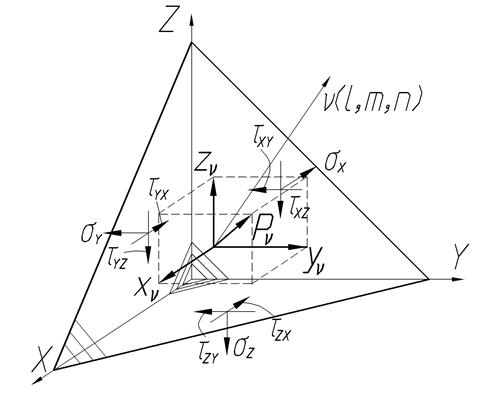
Понятие о тензоре напряжений

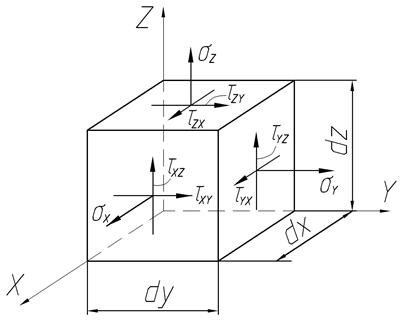
Полное напряжение 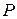, возникающее на площадке, может быть разложено на три составляющие: на одно нормальное напряжение 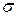и два касательных напряжения 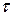. Нормальное напряжение обозначается с индексом, соответствующим осям 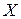, , 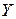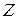( 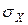, , 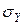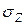). Касательное напряжение обозначается с двумя индексами: первый соответствует оси перпендикулярной к площадке, а второй – оси, вдоль которой направлен вектор ( , , , , , ,).

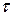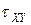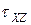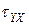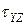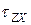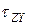Напряженное состояние в точке полностью определяется девятью компонентами напряжений, совокупность которых носит название тензор напряжений:

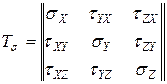
Есть одна важнейшая особенность, заключающаяся в том, что объект 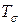– не матрица. Дело в том, что физические величины 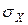, , 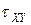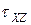и т.д. – не просто абстрактные числа как в матрице, а компоненты (проекции) векторов полных напряжений, действующих на трех гранях элементарного объема.

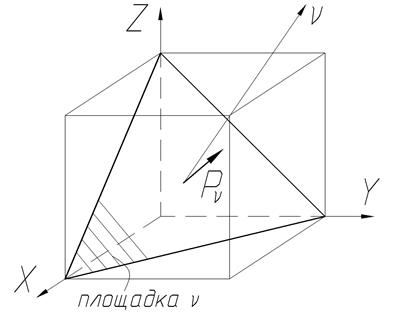
Пусть элементарный объем будет ограничен площадкой 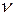. Такая фигура называется тетраэдр.

К этой площадке проведена нормаль .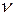

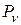– полное напряжение, действующее на площадке .

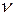Пусть направляющие косинусы между нормалями 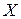, , 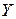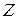и и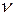меют значения , , .

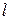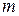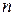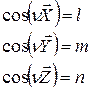(7.2)

7.2 это направляющие косинусы площадки .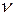

Определим площади площадок 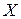, , 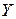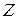через площадь площадки .

, , .

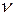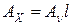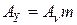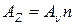Полное напряжение 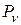раскладывается на проекции

, , .

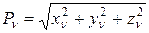
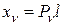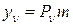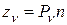Составляющие полного напряжения находятся из условия равновесия тетраэдра

;

;

;

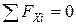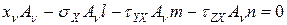
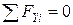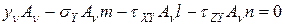
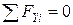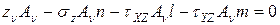
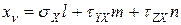
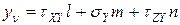(7.3)

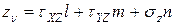
Важность выражений 7.3 заключается в том, что можно найти напряжения, действующие на любой наклонной площадке, зная лишь ее ориентацию.

16)Главные площадки и гл. напряжения. Кубическое уравнение для гл. напряжений. Инварианты тензора напряжений. Типы напряженных состояний: линейное, плоское, объемное