Диаграмма напряженного состояния

Рассмотрим объемное напряженное состояние, представленное главными напряжениями 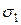, 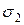и .

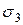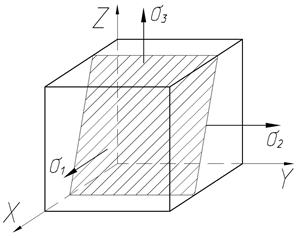
Возвращаясь к формулам 7.8, 7.9 для определения напряжений на площадке общего положения, взятой из семейства площадок параллельного одной из главных осей имеем

; .

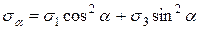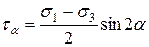Принимая во внимания тригонометрические соотношения

; ,

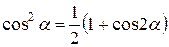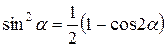получим

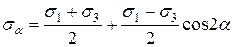(7.10)

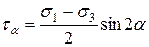. (7.11)

Уравнение 7.10 перегруппируем и обе части уравнений 7.10 и 7.11 возведем в квадрат

.

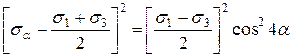
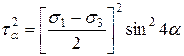Сложив левые и правые части, получим

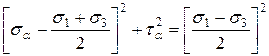(7.12)

Уравнение 7.12 является уравнением окружности в системе координат 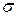, , 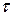заданное в параметрическом виде. Роль параметра играет угол 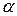. Центр этой окружности находится на оси 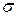на расстоянии 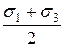. Радиус равен полуразности главных напряжений. Полученный круг называется кругом Мора или круговой диаграммой напряженного состояния.

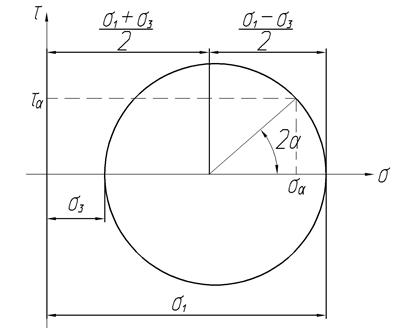
Полученный круг построен для семейства площадок, параллельных вектору 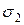. Аналогично можно построить круги Мора для семейств площадок, параллельных векторам 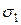и 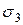. Таким образом может быть построено три круга Мора. Поскольку знак 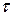не оговаривается, ограничиваются построением только верхней половины круга.

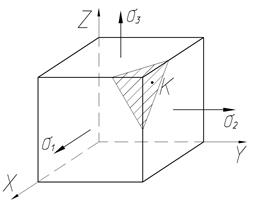
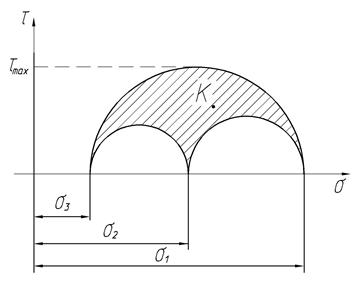
Каждой точке любой окружности соответствует определенная секущая площадка в соответствующем семействе. Но для площадки общего положения соответствует точка 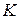на плоскости ( 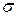, 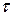), лежащая внутри заштрихованной области, образованной тремя совмещенными кругами Мора, построенными для площадок, параллельных главным осям и проходящих через данную точку .

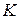Поскольку ни одна из точек не выходит за пределы заштрихованной области, то наибольшее касательное напряжение равно радиусу наибольшего круга

.

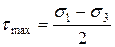======================= 11 ========================