Первичная обработка результатов наблюдений

Если из генеральной совокупности извлечена выборка, состоящая из п чисел (при этом п называется объемом выборки), в которой число х₁ повторяется п₁ раз, число х₂ – п₂ раза,…, число х_k – n_k раз (то есть выборка содержит k различных значений случайной величины), то числа x_i называются вариантами, соответствующие им n_i – частотами, а последовательность вариант, записанных в порядке возрастания, и относящихся к ним частот – статистическим рядом. При этом вместо абсолютных частот n_i можно задавать распределение относительных частот W_i. Если разделить каждую частоту на объем выборки, то получим относительные частотыW_i.

Если исследуется некоторый непрерывный признак, то вариационный ряд может состоять из очень большого количества чисел. В этом случае удобнее использовать группированную выборку. Для ее получения интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько равных частичных интервалов длиной h, а затем находят для каждого частичного интервала n_i – сумму частот вариант, попавших в i-й интервал. Составленная по этим результатам таблица называется группированным статистическим рядом

Полигоном частот, или точки (рис.1) называют ломанную, отрезки которой соединяют точки (х₁, n₁), (х₂, n₂), ... , где х_i – варианты выборки, n_i – соответствующие им частоты. Для построения полигона частот на оси абсцисс откладывают варианты х_i, а на оси ординат – соответствующие им частоты n_i. Точки (х_i,n_i) соединяют отрезками прямых и получают полигон частот (рисунок – 5.1)

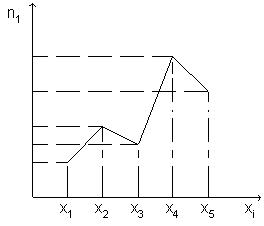
Рисунок 5.1 – Полигон частот

В случае непрерывного признака целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько интервалов длиной h и находят для каждого частичного интервала n_i – сумму частот вариант, попавших в i-тый интервал.

Для непрерывного признака графической иллюстрацией служит гистограмма, то есть ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высотами – отрезки длиной n_i /h (гистограмма частот) или w_i /h(гистограмма относительных частот). Площадь i - го частичного прямоугольника равна hW_i / h = W_i ̶ относительной частоте вариант попавших в i - й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.(рисунок 5.2)

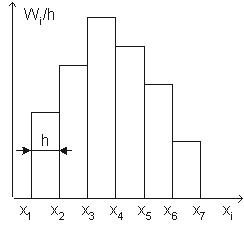
Рисунок 5.2 – Гистограмма