Нормальный (гауссов) закон распределения

Нормальный закон распределения (закон Гаусса) играет исключительно важную роль в теории вероятностей. Это наиболее часто встречающийся на практике закон распределения случайных величин. Главная особенность, выделяющая закон Гаусса, состоит в том, что он является предельным законом, к которому приближаются другие законы при весьма часто встречающихся типичных условиях.

Доказано, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма не жестких ограничениях) приближенно подчиняется нормальному закону. И это свойство выполняется тем точнее, чем большее количество случайных величин суммируется.

Непрерывная случайная величина х имеет нормальный закон распределения (закон Гаусса) с параметрами α и σ, если ее плотность вероятности определена на всей числовой оси 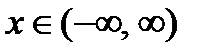и имеет вид:

,

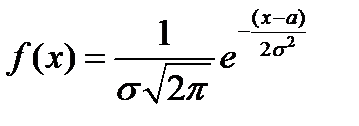Где - среднеквадратическое отклонение случайных величин.

Кривую нормального закона распределения называют нормальной или гауссовой кривой (рисунок 3.1). Гауссова кривая имеет симметричный холмообразный вид с максимумом в точке , причем сам максимум равен:

,

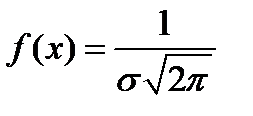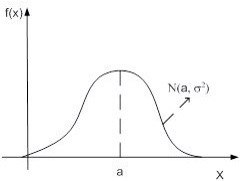
Рисунок 3.1 – Нормальное распределение

Если результат наблюдения является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то при увеличении числа слагаемых распределение центрированного и нормированного результата стремится к нормальному. Этот закон теории вероятностей имеет следствием широкое распространение нормального распределения, что и стало одной из причин его наименования.