Процессов в идеальном газе

№ п/п	Наименование процесса	Условие (свойство) процесса	Вид условия политропы: p υn = const	Значение n
	Изобарный	p = const	pυ0 = const (т.к. υ0 = 1)	n = 0
	Изотермический	T = const или pυ = const	pυ1 = const	n = 1
	Адиабатный	q = 0 (pυk = const)	pυk = const	n = k
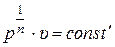
	Изохорный	υ = const	pυn = const	n = 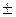∞ (т.к. )

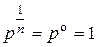Данные таблицы 15.1 можно проиллюстрировать в рυ – координатах с помощью рис. 15.9, где изображены графики всех четырёх основных термодинамических процессов.

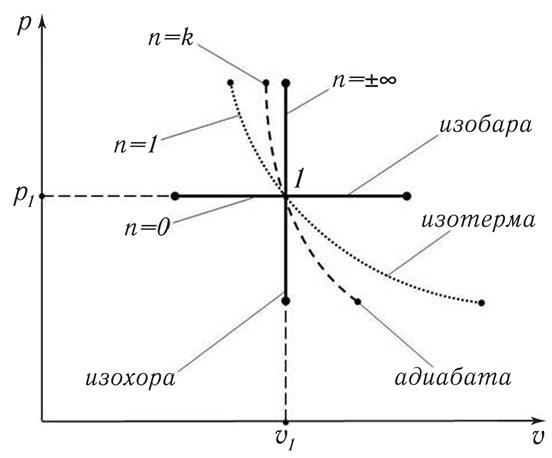
Рис. 15.9. Основные термодинамические процессы (табл. 15.1),

соответствующие значениям показателя политропы n

Из рис. 15.9 видно, что положение графиков на рυ – плоскости монотонно меняется с ростом значения показателя политропы n: от горизонтальной линии, при n = 0, до вертикальной – при n = ∞.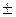

Очевидно, что промежуточным значениям n на рис. 15.1 будут соответствовать промежуточные графики процессов. Например, если 0 < n < 1, то график политропы будет проходить между изобарой и изотермой.

Такое свойство позволяет с помощью политропного процесса описать в рυ – координатах отдельные участки у любого процесса, что часто применяется в расчётах.

Примечание:

Формула для удельной теплоёмкости идеального газа в политропном процессе (15.59) позволяет построить график зависимости с от показателя политропы n, которая имеет вид, приведённый на рис. 15.10.

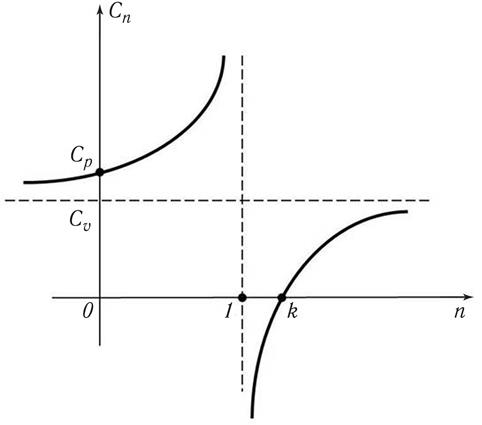
Рис.15.10. Зависимость с_n от n :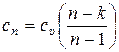

с_р, с_υ и k – удельные теплоёмкости при постоянном давлении, объёме и показателе адиабаты некоторого газа (например, азота) соответственно

Анализ графика на рис. 15.2 показывает:

• если n = k (адиабатный процесс), то c_n = 0;

• если n < 1 и n > k, то c_n >0;

• если 1 < n < k, то c_n < 0;

• если n = 1 + 0 (изотермический процесс), то c_n = +∞;

• если n = 1 – 0 (изотермический процесс), то c_n = –∞;

Таким образом, видно, что у одного газа теплоёмкость существенно меняется в зависимости от того, в каком процессе к нему подводится (или отводится) теплота.