Адиабатный процесс

Условие отсутствия подвода и отвода теплоты к системе называется условием адиабатности процесса.

На практике к адиабатным процессам приближаются такие процессы, в которых теплообменом между рассматриваемой системой и окружающей средой можно пренебречь.

Пренебречь теплообменом системы с окружающей средой можно в двух основных случаях: во-первых, если создать вокруг системы эффективную теплоизоляцию; во-вторых, если термодинамический процесс протекает достаточно быстро, в результате чего система за время процесса не успевает не получить из окружающей среды, ни передать ей сколько-нибудь значительное количество теплоты по сравнению с работой, совершаемой в данном процессе.

Исходная система уравнений (14.6) для адиабатного процесса с дополнительным условием имеет вид:

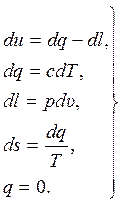(15.27)

Первое и третье уравнения и последнее условие, с учётом свойства идеального газа (10.16), позволяют записать:

du + dl = c_υ dT + p dυ = 0. (15.28)

Подставляя в (15.28) давление р, выраженное из уравнения состояния идеального газа, получаем:

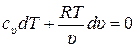. (15.29)

Преобразуем (15.29) к виду:

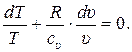(15.30)

После интегрирования (15.30) получаем:

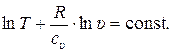(15.31)

Воспользовавшись уравнением Майера (10.18) преобразуем отношение 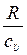к виду:

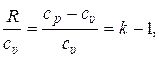(15.32)

где 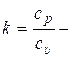называется показателем адиабаты (безразмерная величина).

С учетом (15.32) преобразуем (15.31) к виду:

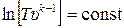. (15.33)

Очевидно, что из (15.33) следует:

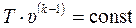. (15.34)

Преобразуем (15.34) следующим образом, учитывая уравнение идеального газа:

,

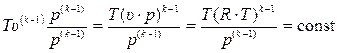или

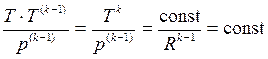. (15.35)

Выражение (15.35) возводим в степень 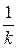. В результате получаем:

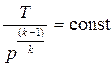. (15.36)

Выразим Т из уравнения состояния идеального газа и подставим в (15.34):

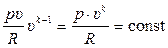
или

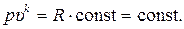(15.37)

Выражения (15.34), (15.36) и (15.37) показывают, как параметры состояния идеального газа (газовой смеси) связаны между собой во время адиабатного процесса. (Вспомним, что для изотермического процесса аналогичная связь имеет вид: р υ = const). В частности, выражение (15.37) справедливо как для начального, так и конечного состояния системы в точках 1 и 2:

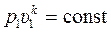и ,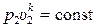

отсюда следует, что

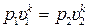. (15.38)

Аналогичным образом из (15.34) и (15.36) получаем:

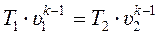или 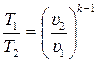, (15.34)

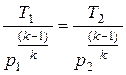или 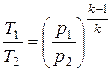. (15.40)

Уравнение (15.37) называется уравнением адиабаты, которое говорит о том, что в ходе адиабатного процесса произведение давления на удельный объём в степени k остаётся постоянным.

Из уравнения адиабаты (15.37) следует, что в р υ-координатах адиабатный процесс отображается степенной функцией вида :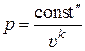

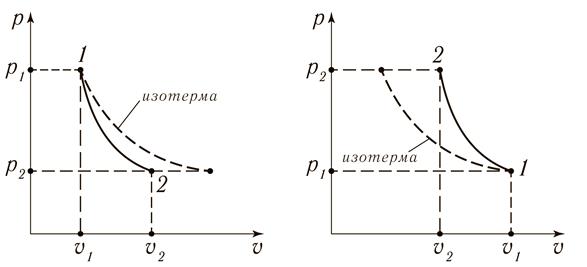
а) б)

Рис. 15.7. Адиабатный процесс 1 – 2 в рυ – координатах:

а) расширение газа; б) сжатие газа

На рис. 15.7 пунктирной линией изображена изотерма (равнобокая гипербола). Очевидно, что график адиабаты круче графика изотермы.

В результате интегрирования (15.28) получаем:

,

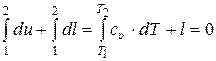или, с учётом (15.32):

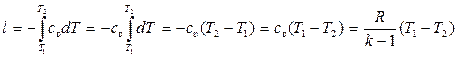. (15.41)

Формулу (15.41), используя уравнение идеального газа, можно преобразовать к виду:

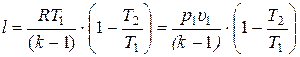, (15.42)

или

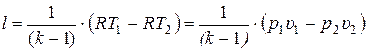. (15.43)

Выводы:

1) Из (15.41) следует, что в адиабатном процессе работа совершается только за счёт уменьшения внутренней энергии.

2) Из последнего условия q = 0 следует, что dq = 0, а значит 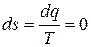. Это означает, что s = const, т.е. в адиабатном процессе энтропия не изменяется.

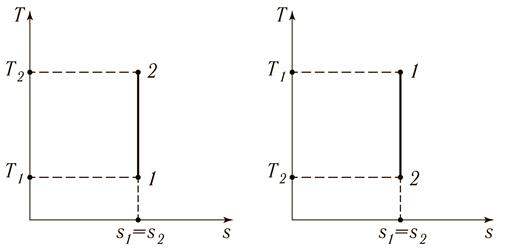
Рис. 15.8. Адиабатный процесс в Ts-координатах