Изохорный процесс

Условие, определяющее изохорный процесс: υ = const или dυ = 0.

Изображение изохорного процесса в рυ – координатах представлено на рис. 15.1 а) и б).

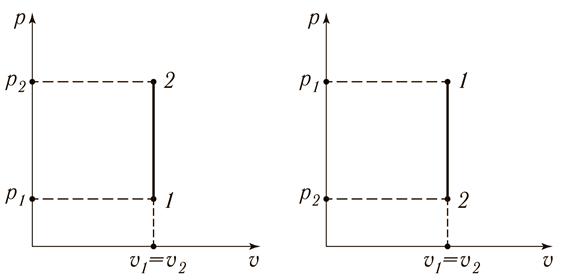
а) б)

Рис. 15.1. Изображение изохорного процесса в рυ – координатах:

а) с повышением давления; б) с понижением давления

Связь между параметрами состояния газа в начале и конце изохорного процесса получаем из уравнения состояния (14.1), записав его для точек 1 и 2:

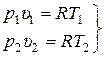. (15.1)

Разделив левые и правые части (15.1) друг на друга получаем:

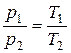. (15.2)

Для рассматриваемого случая общая система уравнений с дополнительным условием принимает следующий вид:

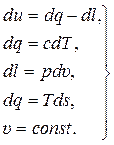(15.3)

Так как при условии υ = const неизвестная в общем случае удельная теплоёмкость процесса с превращается в известную (из справочника) удельную теплоёмкость при постоянном объёме с_υ, то в системе (15.3) число неизвестных функций становится равным числу независимых уравнений. То есть система (15.3) становится однозначно разрешимой. Решение дифференциальных уравнений производится, как известно, путём их интегрирования.

После интегрирования второго уравнения (15.3) с учётом, что с = с_υ (для наглядности здесь и далее будем считать удельные теплоёмкости с_υ и с_р постоянными величинами), будем иметь:

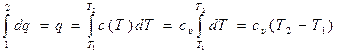, (15.4)

где Т₁ и Т₂ – температуры газа в начале и конце процесса соответственно, К.

После интегрирования третьего уравнения (15.3) получаем:

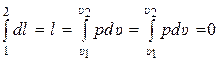, (15.5)

где υ₁ и υ₂ – удельные объёмы газа в начале и конце процесса соответственно (υ₁ = υ₂), м³/кг.

После интегрирования первого уравнения (15.3) получаем, с учётом (15.5):

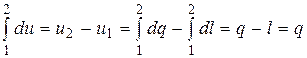. (15.6)

После интегрирования четвёртого уравнения (15.3) получаем:

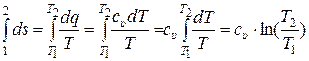. (15.7)

Выводы:

1) Из (15.2) следует, что в изохорном процессе отношение давлений равно отношению температур.

2) Из(15.5) следует, что в изохорном процессе работа не совершается (удельная работа равна нулю). (Так как при интегрировании уравнение идеального газа не использовалось, то этот вывод справедлив для всех случаев: идеального газа, реального газа, для вещества в твёрдой или жидкой фазах).

3) Из (15.6) следует, что в изохорном процессе вся теплота процесса идёт на изменение внутренней энергии газа. (Это также справедливо для всех случаев).

4) Из (15.7) следует, что в Ts – координатах изохорный процесс изображается логарифмической кривой рис. 15.2 а) и б).

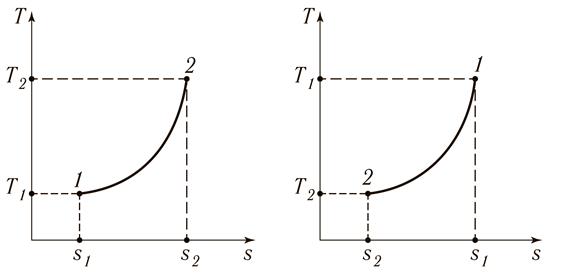
а) б)

Рис. 15.2. Изображение изохорного процесса в T s-координатах:

а) с подводом теплоты; б) с отводом теплоты