Второй закон термодинамики. Второй закон термодинамики, как и первый, установлен экспериментально.

Второй закон термодинамики, как и первый, установлен экспериментально.

В теоретических работах приводятся различные формулировки второго закона, которые, по сути, являются обобщенными интерпретациями наблюдаемых в природе явлений.

При этом сами формулировки являются эквивалентными: исходя из какой-то одной можно доказать справедливость других.

Второй закон относится к неравновесным (необратимым)термодинамическим процессам – устанавливает признаки, отличающие их от равновесных (обратимых) процессов.

Второй закон термодинамики может быть сформулирован следующим образом:

изменение удельной энтропии термодинамической системы в неравновесном (необратимом) процессе Δs_н всегда больше изменения энтропии в аналогичном равновесном процессе:

Δs_н > Δs_р. (12.1)

Это означает, в частности, следующее. Если в некотором равновесном (необратимом) процессе термодинамическая система благодаря подводу теплоты в количестве q переходит из начального состояния 1 в конечное состояние 2, и её удельная энтропия при этом меняется от s₁ до s₂, то это изменение, в соответствии с результатом интегрирования (11.2), будет определяться соотношением:

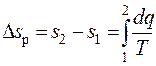, (12.2)

где Δs_p − изменение удельной энтропии в результате равновесного процесса 1 − 2, Дж/(кг∙К).

Если же переход термодинамической системы из того же начального состояния 1 произойдёт, при той же подведенной теплоте, в неравновесном (необратимом) процессе в другое конечное состояния 2′, то, согласно принципу возрастания энтропии (12.1), будет справедливо неравенство:

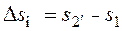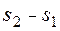> (12.3)

или, с учётом (12.2):

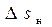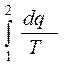> , (12.4)

где Δs_н – изменение удельной энтропии в результате неравновесного (необратимого) процесса 1 – 2′, Дж/(кг · К); 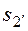– значение удельной энтропии системы в конце неравновесного процесса 1 − 2′ подвода теплоты q (оно определяется после того, как система пришла в новое равновесное состояние 2′ через какое-то время после окончания неравновесного процесса), Дж/(кг ∙ К).

Из принципа возрастания энтропии также вытекает следующее. Если в некотором равновесном процессе 1 − 2 к системе из окружающей среды подводится удельная работа в количестве l, Дж/кг, (энергия в форме работы), то, как было отмечено выше, ее энтропия не изменяется, т.е.:

Ds_р = s₂ – s₁ = 0. (12.5)

Если такое же количество энергии в виде работы подводится из окружающей среды к системе в некотором неравновесном (необратимом) процессе 1 − 2′, который начинается из того же начального состояние системы 1, то её энтропия, в соответствии с (12.1), обязательно возрастёт, т. е. будет справедливо неравенство: 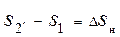> 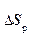, или, с учетом (12.5):

Ds_н > 0, (12.6)

где 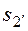– значение удельной энтропии в конце неравновесного (необратимого) процесса 1 − 2′ подведения того же количества удельной работы l, Дж/кг, (оно определяется после того, как система пришла в новое состояние равновесия 2′ через какое-то время после завершения неравновесного процесса), Дж/(кг·К).

Данное возрастание энтропии объясняется тем, что в неравновесном (необратимом)процессе часть переданной из внешней среды работы обязательно самопроизвольно превращается в теплоту (например, благодаря наличию сил трения в реальных системах). То есть, в результате такого неравновесного процесса часть энергии, поступившей к системе из внешней среды, обязательно поступит к ней в форме теплоты, что обязательно приведет к росту ее энтропии (последнее следует из самого определения энтропии).

Очевидно, что для принципа возрастания энтропии варианты, когда теплота и работа отводятся от термодинамической системы в некоторых неравновесных процессах, могут быть рассмотрены аналогичным образом.

Если аналитически обобщить оба принципа существования (11.2) и возрастания (12.1) энтропии в форме одного соотношения, то можно записать:

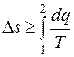, (12.7)

где Ds – конечное изменение удельной энтропии системы в любом (равновесном или неравновесном) процессе в результате подвода или отвода удельных теплоты q и работы l, Дж/(кг·К); dq - дифференциал (бесконечно малое количество) удельной теплоты, подводимой к термодинамической системе или отводимой от неё в случае, когда вся эта теплота q подводится к рассматриваемой системе (или отводится от неё) в условиях равновесного процесса, Дж/кг; Т - текущая температура системы в условиях реализации равновесного процесса подвода теплоты q, К.

В соотношении (12.7) знак равенства относится к равновесным процессам, а знак неравенства − к неравновесным.

Например, для процессов, когда из внешней среды теплота к системе не подводится и от неё не отводится, из (12.7) следует:

Δs ≥ 0. (12.8)

О таких процессах говорят, что они протекают в адиабатных условиях.

Из (12.8) следует, что если внутри термодинамической системы осуществляется какой-то неравновесный процесс, а сама система находится в адиабатных условиях, то её энтропия возрастает, так как в этом случае Δs > 0.

Изолированная термодинамическая система, по определению, не обменивается с окружающей средой никакой энергией, в том числе и энергией в форме теплоты. Таким образом, все процессы, происходящие в ней, протекают в адиабатных условиях.

Из сказанного выше вытекает важное следствие: