Первый закон термодинамики в дифференциальном виде.

Формула для расчёта механической работы

при изменении объёма системы

Выражение (8.2) можно рассматривать как интегральную форму записи первого закона термодинамики.

Анализировать различные термодинамические процессы удобно, если пользоваться не интегральной, а дифференциальной формой записи первого закона термодинамики. В частности, это даёт возможность рассчитывать величину l – удельную работу процесса или, более строго, удельную энергию, подведённую к системе или отведённую от неё в форме механической работы.

Дифференциальная форма записи справедлива только для равновесных процессов. Рассмотрим её вывод из (8.2) для произвольного равновесного процесса изменения объёма некоторой термодинамической системы. Такой системой, в частности, может быть некоторый объём газа.

Известно, что равновесный процесс может быть изображён непрерывной кривой, например, в рυ – координатах (рис. 9.1). Это будет р = р (υ) – уравнение процесса, описывающее зависимость абсолютного давления системы р, Па, в ходе процесса, от удельного объёма υ, м³/кг.

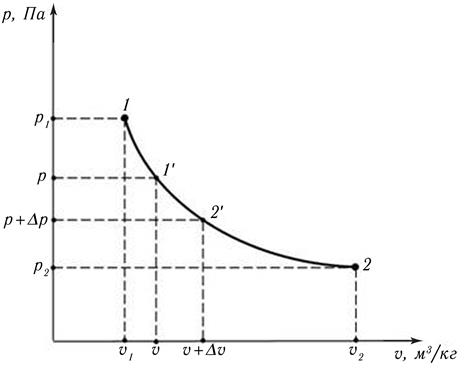
Рис. 9.1. Равновесный процесс в рυ – координатах

Для некоторой системы, в которой реализуется процесс 1 – 2, первый закон термодинамики (8.1) запишется в виде:

U₂ – U₁ = Q – L, Дж. (9.1)

На кривой р(υ) выберем произвольную промежуточную точку 1′ с параметрами р и υ. Рассмотрим малую часть процесса 1 – 2 в районе точки 1′, т.е. процесс 1′ – 2′, при котором параметры состояния изменяются на малые величины Δр и Δυ.

Для малого процесса 1′ – 2′ запишем первый закон термодинамики в виде:

(U +ΔU) – U = ΔQ – ΔL, (9.2)

где U и U +ΔU – внутренние энергии системы в точках 1′ и 2′ соответственно, Дж; ΔU – изменение внутренней энергии системы в процессе 1′ → 2′, Дж; ΔQ – теплота процесса 1′ – 2′, Дж; ΔL – работа процесса 1′ – 2′, Дж.

Из (9.2) получаем:

ΔU = ΔQ – ΔL, (9.3)

Для определения ΔL схематично изобразим систему в точках 1′ (сплошная линия) и 2′ (пунктирная линия) на рис. 9.2.

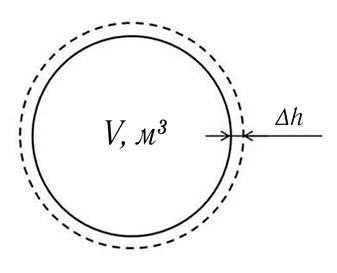
Рис. 9.2. Схема процесса 1′ – 2′:

V – объём системы в точке 1′; Δh – перемещение поверхности системы в процессе 1′ – 2′

Исходя из определения механической работы, можем записать:

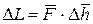, (9.4)

где 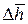– среднее перемещение поверхности системы в малом процессе 1′ – 2′, м; 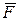– среднее, за время малого процесса 1′ → 2′, значение силы, действующей на поверхность системы, Н.

В силу малости процесса 1′ – 2′, можем записать:

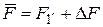, (9.5)

где 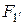– значение силы, действующей на поверхность системы в точке 1′, Н; ΔF – малое приращение, обусловленное изменениями давления и поверхности системы в ходе процесса 1′ – 2′, Н.

Значение 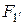определяется по очевидной формуле, при известных давлении системы р, Па, и площади поверхности системы S, м², в точке 1′:

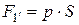. (9.6)

Подставляя (9.5) и (9.6) в (9.4) получаем:

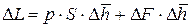. (9.7)

В (9.7) перейдём к пределу при Δр (а значит и Δυ) стремящемся к нулю:

lim ΔL = p · S · lim 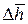+ lim (ΔF · ).

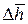Δυ→0 Δυ→0 Δυ→0

Δp→0

В результате, отбросив по очевидным причинам бесконечно малые величины второго порядка малости, получаем:

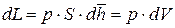, (9.8)

где dL – дифференциал механической работы в процессе 1 – 2, Дж; 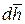– дифференциал среднего перемещения поверхности системы в ходе процесса 1 – 2, м; dV – дифференциал изменяющегося в ходе процесса 1 – 2 объёма системы, 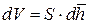, м³.

Замечание:

Для наглядности проиллюстрируем справедливость выражения 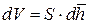для частного случая, когда система имеет сферический объем:

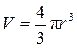. (9.9)

Будем считать, что сфера «раздувается», то есть её радиус изменяется. После дифференцирования (9.9) получаем формулу для бесконечно малого приращения объёма «раздувающейся» сферы:

,

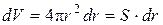где S – площадь сферы, м²; dr – дифференциал (бесконечно малое приращение) радиуса сферы, м.

Переходя в (9.3) к пределу при Δр (и Δυ) стремящихся к нулю и подставляя (9.8) будем иметь:

dU = dQ – dL = dQ – p dV. (9.10)

где dU, dQ и dL – дифференциалы (бесконечно малые приращения) внутренней энергии системы, теплоты и работы процесса соответственно, Дж.

Выражение (9.10) является дифференциальной формой записи первого закона термодинамики.

Разделив обе части (9.10), например, на массу системы, получаем уравнение для удельных величин:

du = dq – dl = dq – p dυ, (9.11)

где dυ – дифференциал удельного объема системы, м³/кг.

Таким образом, удельная механическая работа рассчитывается путём интегрирования дифференциального уравнения вида:

dl = p dυ, (9.12)

где р = p(υ) – уравнение процесса. В примере, изображённом на рис. 9.1. это процесс 1 – 2.

После интегрирования (9.12) от начала в точке 1 до конца процесса в точке 2 получаем формулу для расчёта удельной работы любого процесса 1 – 2:

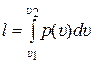. (9.13)

где υ₁ и υ₂ – значения удельного объёма в начале и конце процесса 1 – 2 соответственно, м³/кг.

Из геометрической интерпретации интеграла следует, что значение удельной работы, рассчитываемое по (9.13), равно площади под уравнением процесса р(υ) в рυ – координатах. На рис. 9.1 это площадь под линией процесса 1 – 2.

Для того чтобы по формуле (9.13) вычислить значение удельной работы необходимо знать вид функции р(υ) и пределы интегрирования υ₁ и υ₂.