Открытие энтропии

Примерно в 1860 году немецкий физик Клазиус, изучая тепловые процессы впервые пришёл к следующему выводу. У каждой термодинамической системы существует такая функция состояния, которая в ходе равновесного процесса изменяется только тогда, когда энергия к системе подводится или отводится в форме теплоты. Причём это изменение происходит таким образом, что, всегда выполняется равенство:

dQ = T · dS, (11.1)

где dQ – дифференциал (бесконечно малое приращение) теплоты, которая подводится к системе, Дж; Т – текущая температура системы, К; dS – дифференциал открытой Клазиусом новой функции состояния термодинамической системы, Дж/К.

Функцию S назвали э н т р о п и′ я. Термин греческого происхождения, который означает поворот, превращение, поворачиваюсь внутрь, способность к превращению.

Запишем (11.1) в более удобной форме для удельных величин. Для этого поделим обе части (11.1) на массу системы М, кг:

dq = T · ds,

или

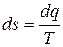, (11.2)

где q – удельная теплота процесса, Дж/кг; s – функция состояния - удельная энтропия, Дж/(кг·К).

Так как энтропия является функцией состояния, то это означает, что она является непрерывной функцией каких-то двух из трёх (р, υ, Т) параметров состояния. То есть её значение однозначно определено, например, в каждой точке рυ-плоскости. Следовательно, разность энтропий в двух разных точках определяется только положением этих точек на рυ-плоскости и не зависит от вида уравнения процесса перехода из одной точки в другую.

Докажем это, исходя из первого закона термодинамики в дифференциальном виде (9.11). Как уже отмечалось, выражение (9.11) описывает равновесные процессы, протекающие в любых термодинамических системах: в системах, находящихся в состоянии идеального газа; в системах, находящихся в состоянии реальных газов; в системах, находящихся в жидкой или твёрдой фазах. Запишем (9.11) в виде:

dq = du + p · dυ, (11.3)

где q – удельная теплота процесса, Дж/кг; u – удельная внутренняя энергия системы, Дж/кг; p – давление внутри системы, Па; υ – удельный объём системы, м³/кг.

Вначале рассмотрим доказательство справедливости утверждения (11.2) для случая, когда систему можно рассматривать как идеальный газ, то есть когда уравнение состояния системы имеет вид (см. раздел 2):

p υ = R T. (11.4)

Из (11.4) получаем:

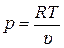. (11.5)

Обе части (11.3) делим на Т:

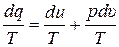. (11.6)

Подставляем в правую часть (11.6) формулы для идеального газа (11.5) и (10.16) получаем:

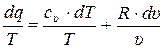. (11.7)

Для наглядности будем считать с_υ постоянной величиной.

Введём в рассмотрение новую непрерывную функцию двух параметров состояния s следующего вида:

s = с_υ ln T + R ln υ + const. (11.8)

Очевидно, что:

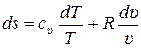. (11.9)

Сравнивая (11.9) и (11.7) получаем:

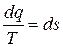или dq = T·ds, (11.10)

где s – некоторая новая функция состояния системы – непрерывная функция двух параметров состояния (11.8), Дж/(кг·К).

Полученное из первого закона термодинамики выражение (11.10) является доказательством справедливости утверждения (11.2) для идеальных газов. Справедливость утверждения (11.2) для других термодинамических систем (реальных газов, жидких и твёрдых тел) приводится в
Приложении 6.

Таким образом, выражение (11.2) можно рассматривать как определение удельной энтропиитермодинамической системы.

Для всех технически значимых веществ значения удельной энтропии определены на базе экспериментальных данных. Эти значения приводятся в справочной литературе в виде таблиц, например, в виде зависимости удельной энтропии от давления и температуры s = s (p, T).

Пример:

Рассмотрим, как можно экспериментальным методом (на основе экспериментальных данных) определить изменение удельной энтропии газа. Экспериментальные данные – это его удельная теплоёмкость при постоянном давлении с_р. Для наглядности будем считать с_р известной постоянной величиной.

Будем рассматривать некий процесс 1 – 2 при р = const, в котором к газу подводится теплота q.

По определению удельной теплоёмкости для такого процесса можем записать:

dq = с_р dT. (11.11)

С другой стороны, по определению удельной энтропии имеем:

dq = T·ds. (11.12)

Сравнивая (11.12) и (11 11) получаем:

с_р dT = T·ds или 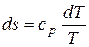. (11.13)

После интегрирования (11.13) в пределах процесса 1 – 2 получаем:

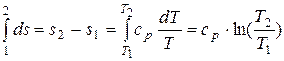. (11.14)

На базе подобных экспериментальных данных могут быть построены таблицы для энтропии, как функции температуры и давления.

Примечание:

1) Воспользовавшись определением удельной энтропии (11.2) запишем первый закон термодинамики в виде:

du = dq – dl = T ds – p dυ. (11.15)

Из (11.15) видно, что s – величина, сопряженная с Т, подобно тому как υ – величина, сопряжённая с р. То есть s и υ являются экстенсивными величинами, а р и Т – интенсивными. Экстенсивные величины изменяются под воздействием соответствующих интенсивных величин.

2) По определению удельной энтропии (11.2) можем записать:

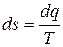. (11.16)

Это означает, что если в элементарном равновесном процессе к 1 кг некоторого вещества подводится энергия в виде теплоты в количестве dq при температуре Т, то это обязательно приведёт к изменению энтропии вещества на .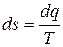

При этом следует отметить, что если в равновесном процессе такое же количество энергии будет подведено к веществу не в виде теплоты dq, а в виде работы dl, то энтропия системы не изменится ds = 0.