Общие сведения. В термодинамике теплоёмкость веществ определяется для всех агрегатных состояний: твёрдого, жидкого и газообразного

В термодинамике теплоёмкость веществ определяется для всех агрегатных состояний: твёрдого, жидкого и газообразного. Например, у воды теплоёмкость жидкой фазы примерно в два раза больше, чем газовой – когда вода находится в виде пара.

Строго говоря, под теплоёмкостью термодинамической системы следует понимать её энергоёмкость в процессах, когда энергия к ней подводится в форме теплоты (по механизму теплообмена).

Забегая вперёд, отметим, что теплоёмкости всех веществ, значимых для техники, экспериментально определены и их значения приводятся в справочной литературе. Знание теплоёмкости вещества необходимо, главным образом для того, чтобы иметь возможность рассчитывать теплоту, которую необходимо подвести к веществу, чтобы нагреть его до определённой температуры или отвести от вещества, при его охлаждении.

Если к некоторому количеству вещества массой М, кг, подвести теплоту в количестве Q, Дж, то его температура возрастет от начальной Т₁ до конечной Т₂, К.

Определение:

Отношение 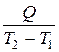называется средней теплоёмкостью С_m в данном процессе в интервале температур от Т₁ до Т₂:

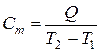,Дж/К. (10.1)

Из опытов известно, что в различных процессах для нагрева одного и того же вещества в одном и том же интервале температур требуются различныеколичества теплоты. Например, при нагреве газа при постоянном давлении теплоты потребуется больше, чем при его нагреве при постоянном объёме. Это означает, что теплоёмкость зависит от вида процесса, в котором осуществляется нагрев.

Как будет показано ниже, наибольшее практическое значение имеют теплоёмкости вещества, определяемые в двух процессах: при постоянном удельном объёме υ = const; при постоянном абсолютном давлении р = const.

Чаще всего в теплотехнических расчётах пользуются удельными массовыми теплоёмкостями.

Формула для определения средней удельной массовой теплоёмкости с_m в диапазоне температур от Т₁ до Т₂ получается из (10.1) путём деления обоих частей равенства на массу вещества М:

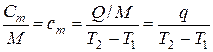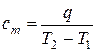, или , Дж/(кг · К), (10.2)

где q – теплота, которую необходимо подвести к 1 кг вещества, чтобы изменить его температуру от Т₁ до Т₂, Дж/кг.

Примечание:

1) По своему физическому смыслу средняя удельная массовая теплоёмкость – это количество теплоты, которое необходимо подвести к 1 кг вещества, чтобы нагреть его на один градус.

2) Помимо удельных массовых в расчётах используются также удельные объёмные и удельные мольные теплоёмкости (подробнее об этом см. Приложение 5).

Средняя удельная теплоёмкость является свойством конкретного вещества и для данного процесса зависит только от интервала температур ΔТ = Т₁ – Т₂, в котором определяется.

В термодинамике, для удобства расчётов, дополнительно вводится понятие истинной удельной массовой теплоёмкости с, Дж/(кг·К).

Отличие в определении истинной теплоёмкости от средней состоит только в том, что истинная определяется по тем же соотношениям (10.1) и (10.2), но при условии, что изменение температуры вещества в ходе процесса стремится к нулю: (Т₂ – Т₁) = ΔТ → 0. То есть ширина интервала «стягивается» к точке Т₁. Следовательно, можно сказать, что истинная теплоёмкость определяется не в интервале температур, а в точке – при одной какой-то температуре. Соответственно и зависеть она будет не от интервала температур как средняя, а просто от температуры – то есть будет является непрерывной функцией температуры, так как при разных температурах, в общем случае, значение истинной теплоёмкости будет разным.

Очевидно, что если в (10.2) знаменатель (Т₂ – Т₂) = ΔТ стремится к нулю, то и числитель q также будет стремиться к нулю. Из высшей математики известно, что предел такого отношения равен производной от функции q, зависящей от Т, по переменной Т:

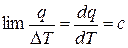, Дж/(кг · К). (10.3)

ΔТ→0

Соотношение (10.3) можно считать определением истинной удельной массовой теплоёмкости, по которому на базе экспериментальных данных определяются её значения.

Соотношение (10.3) можно преобразовать к виду, удобному для расчёта теплоты процесса:

dq = c(T) dT. (10.4)

Если в результате процесса вещество, к примеру, нагревается от Т₁ до Т₂, то после интегрирования (10.4) в соответствующих пределах получим:

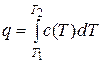, (10.5)

где q – удельная теплота процесса, Дж/кг.

В термодинамике формулы (10.4) и (10.5) являются основными соотношениями для расчёта удельной теплоты в различных процессах.

Примечание:

С учётом (10.4) первый закон термодинамики (9.11) можно теперь записать в виде:

du = c(T) dT – p(υ) dυ.

Очевидно, чтобы воспользоваться соотношением (10.5) необходимо знать функцию с(Т) для данного процесса.

Следует отметить, что, благодаря экспериментам, для всех веществ удельные теплоёмкости при постоянном абсолютном давлении (в дальнейшем для краткости – при постоянном давлении) и при постоянном удельном объёме (в дальнейшем для краткости – при постоянном объёме) известны. Их значения приводятся в справочной литературе в виде таблиц. Зависимость удельной истинной теплоёмкости при постоянном давлении от температуры с_р(Т) для всех технически значимых веществ в твёрдой, жидкой и газовой фазах приводится в виде стандартной формулы:

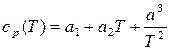, Дж/(кг·К), (10.6)

где a₁, a₂ и a₃ – известные коэффициенты, имеющие своё значение для каждого вещества; Т – абсолютная температура, К.

10.2. Теплоёмкость газов

У одного и того же газа значение теплоёмкости, как уже отмечалось, зависит от вида процесса, в котором теплота к газу подводится.

В технике большую роль играют процессы, протекающие в газах при постоянном объёме υ = const и постоянном давлении р = const.

Средние и истинные удельные теплоёмкости газа для этих процессов определяется в соответствии с (10.2) и (10.3) следующим образом:

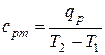, (10.7)

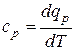, (10.8)

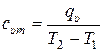, (10.9)

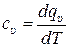, (10.10)

где с_pm и с_р – удельные массовые теплоёмкости газа при постоянном давлении средняя, в интервале температур от Т₁ до Т₂, и истинная соответственно, Дж/(кг·К); q_p и dq_р – удельные теплота и её дифференциал в процессе нагрева газа при постоянном давлении от Т₁ до Т₂, Дж/кг; с_υm и с_υ– удельные массовые теплоёмкости газа при постоянном объёме средняя, в интервале температур от Т₁ до Т₂, и истинная соответственно, Дж/(кг·К); q_υ и dq_υ – удельные теплота и её дифференциал в процессе нагрева газа при постоянном объёме от Т₁ до Т₂, Дж/кг.

Как было отмечено выше, в справочной литературе приводятся таблицы для с_pm и формулы типа (10.6) для с_р.

Также, благодаря экспериментам, для каждого газа известно значение так называемого показателя адиабаты k, который определяется как отношение удельной теплоёмкости при постоянном давлении к удельной теплоёмкости при постоянном объёме:

.

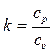Например, для одноатомных газов k = 1,67, для двухатомных k = 1,40, а для трёхатомных и многоатомных k = 1,29. Таким образом, зная с_pm и с_р, а также k, всегда можно вычислить с_υm и с_υ.

Замечание:

Строго говоря, удельная теплоёмкость газа зависит от давления, при котором она определялась. Однако существенно эта зависимость проявляется при очень высоких давлениях, которые в обычных теплотехнических расчётах встречаются редко. То есть в большинстве случаев можно приближённо считать, что удельная теплоёмкость не зависит от давления.

В технике часто встречаются процессы, когда в газе одновременно изменяются и давление, и объём.

Соответственно значение теплоёмкости в таком общем случае нам неизвестно. Однако, забегая вперёд, отметим, что в термодинамике разработана теория политропного процесса, которая позволяет рассчитать теплоёмкость для такого рода процессов.

Подробно эта теория будет изложена ниже в соответствующих разделах.

Смесь идеальных газов, также как и однородные газы, характеризуется удельной теплоёмкостью, которая рассчитывается по известному химическому составу смеси (подробнее см. Приложение 5).

Примечание:

1) Изменение внутренней энергии любого идеального газа в любом равновесном процессе можно вычислить по его истинной удельной теплоёмкости при постоянном объёме с_υ(Т). Покажем это.

Внутренняя энергия, как уже отмечалось, является функцией состояния – непрерывной функцией параметров состояния. По определению дифференциала (бесконечно малого приращения) функции двух переменных можем записать:

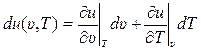, (10.11)

где υ и Т – параметры состояния – удельный объём и абсолютная температура соответственно, м³/кг, К; u (υ, Т) – удельная внутренняя энергия идеального газа, как функция переменных υ и Т, Дж/кг; 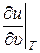и 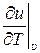– частные производные от внутренней энергии: по удельному объёму, при постоянной температуре, и по температуре, при постоянном удельном объёме, соответственно, Дж/м³, Дж/(кг · К), dυ и dT – дифференциалы удельного объёма и температуры соответственно, м³/кг, К.

Экспериментально установлено, что внутренняя энергия идеальных газов не зависит от их удельного объёма υ. Это означает, что первое слагаемое в (10.11) равно нулю, как производная, взятая от константы. Следовательно, из (10.11) получаем:

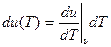. (10.12)

Величина 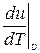характеризует изменение внутренней энергии идеального газа в процессе при постоянном удельном объёме υ = const. Для такого процесса dυ = 0 (как дифференциал от константы). Соответственно первый закон термодинамики для такого процесса при постоянном υ принимает вид:

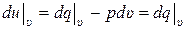. (10.13)

С другой стороны, из определения (10.10) истинной удельной теплоёмкости при постоянном объёме с_υ получаем:

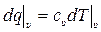. (10.14)

Сравнивая (10.13) и (10.14) будем иметь:

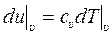, или 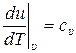. (10.15)

Подставляя (10.15) в (10.12) получаем формулу для вычисления изменения внутренней энергии идеального газа при любых процессах, когда, в общем случае, одновременно могут меняться и давление, и удельный объём:

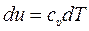. (10.16)

Изменение удельной внутренней энергии идеального газа в некотором процессе 1 – 2 определяется путём интегрирования (10.16) в соответствующих пределах:

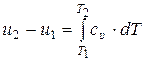, (10.17)

где Т₁ и Т₂ – начальная и конечная температуры идеального газа соответственно, К.

Формула (10.17) показывает, что рассчитать изменение внутренней энергии идеального газа в любом процессе можно по известной истинной удельной теплоёмкости этого газа при постоянном объёме.

2) У идеальных газов удельные теплоёмкости связаны меду собой соотношением:

с_р – с_υ = R, (10.18)

где с_р и с_υ – удельные теплоёмкости при постоянном давлении и при постоянном объёме соответственно (это могут быть либо истинные, либо средние теплоёмкости), Дж/(кг·К); R – газовая постоянная данного идеального газа, Дж/(кг · К).

Докажем справедливость (10.18) опираясь на первый закон термодинамики и свойство идеальных газов (10.16):

dq = du + p dυ = c_υ dT + p dυ. (10.19)

По правилам вычисления дифференциала от произведения имеем:

d (p υ) = p · dυ + υ ·dp. (10.20)

Выражаем из (10.20)(p dυ) и подставляем в (10.19), учитывая, что p υ = R T:

dq = c_υ dT + d (R · T) – υ dp = (c_υ + R) dT – υ dp. (10.21)

Выражение (10.21) справедливо для любых процессов.

Далее будем рассматривать только процессы при постоянном давлении р = const, а значит dp = 0. Для такого процесса (10.21) принимает вид:

dq = (c_υ + R) dT. (10.22)

С другой стороны, для такого процесса из определения с_р – истинной удельной теплоёмкости при постоянном давлении (10.8) следует:

dq = c_р dT. (10.23)

После сравнения (10.22) и (10.23) получаем:

c_р = c_υ + R или c_р – c_υ = R. (10.24)

Выражение (10.24) впервые было получено немецким врачом Майером в 1824 году и называется соотношением Майера. Из него следует, что газовая постоянная некоторого идеального газа (например, азота) равна разности между его удельными теплоёмкостями при постоянном давлении и при постоянном объёме.

10.3. Теплоёмкость твёрдых и жидких тел

Для веществ, находящихся в твёрдом или жидком состояниях, также как и для газов вводятся понятия удельных теплоёмкостей при постоянном давлении и постоянном объёме:

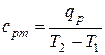, (10.25)

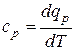, (10.26)

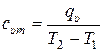, (10.27)

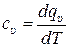. (10.28)

Особенностью жидких и твёрдых тел является то, что в расчётах их можно рассматривать практически несжимаемыми. При любом давлении объём тела остаётся практически неизменны. Следовательно, отличие с_υ и с_р, при их экспериментальном определении, весьма незначительны, и в большинстве инженерных расчётов этим отличием можно пренебречь.

Для всех технически важных твёрдых и жидких веществ в справочной литературе приводится универсальная формула типа (10.6) для истинной удельной теплоёмкости при постоянном давлении:

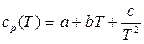, Дж/(кг · К), (10.29)

где a, b и c – известные константы для каждого вещества.

Также для многих веществ приводятся таблицы для средних теплоёмкостей с_pm.

Примечание:

При очень низких температурах теплоёмкость многих веществ рассчитывается по эмпирическому уравнению Дебая [5]:

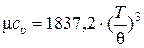, (10.30)

где μс_υ – удельная мольная теплоёмкость при постоянном объёме, кДж/(кмоль·К); θ – температура Дебая, К.

Значения θ для некоторых веществ приводится в табл. 10.1.

Таблица 10.1