Изотермический процесс

Условие, определяющее этот процесс: Т = const или dT = 0.

Примечание:

Как уже отмечалось, из эксперимента известно, что у идеальных газов удельная внутренняя энергия зависит от температуры u = u(T). То же относится к удельной энтальпии, так как:

i = u (T) +p υ = u (T) + RT.

Из этого следует, что изотермический процесс одновременно является процессом при постоянных удельных внутренней энергии и энтальпии идеального газа.

Соотношение между параметрами состояния в изотермическом процессе определяется из уравнения состояния идеального газа. Запишем его для точек 1 и 2 – начала и конца изотермического процесса:

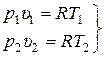. (15.19)

Разделив обе части (15.19) друг на друга получаем:

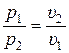. (15.20)

Из (15.20) следует, что при изотермическом процессе давление и удельный объём обратно пропорциональны друг другу. То есть в рυ – координатах графиком изотермического процесса – изотермой является равнобокая гипербола, для которой координатные оси служат асимптотами, рис. 15.5.

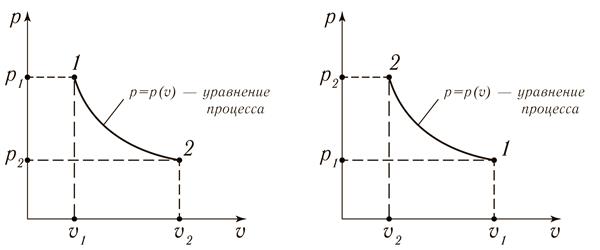
а) б)

Рис. 15.5. Изотермический процесс 1 – 2 в рυ – координатах:

а) расширение газа; б) сжатие газа

Для определённости будем считать, что в ходе изотермического процесса Т = сonst = Т₁. Тогда для любой промежуточной точки процесса 1 – 2 можем записать уравнение состояния идеального газа:

p υ = R T₁ или 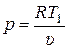. (15.21)

Выражение (15.21), вытекающее из условия Т = const, является уравнением изотермического процесса, которое можно добавить к исходной системе уравнений (14.6). В итоге система уравнений для изотермического процесса имеет вид:

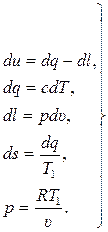(15.22)

В результате интегрирования первого уравнения в (15.22) получаем:

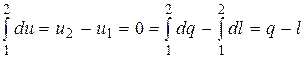или q = l. (15.23)

В результате интегрирования третьего уравнения, с учётом последнего, получаем:

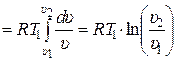. (15.24)

В результате интегрирования четвёртого уравнения получаем:

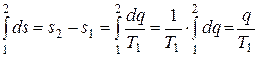. (15.25)

Выводы:

1) Из (15.23) следует, что в изотермическом процессе:

• вся теплота, подводимая к газу, полностью превращается в работу расширения;

• при сжатии газа, от него отводится теплота в количестве, равном работе, затраченной на сжатие.

2) Из (15.23) и (15.24), с учётом (15.20), получаются следующие расчётные формулы:

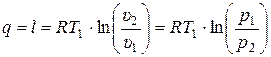. (15.26)

3) Из (15.25), с учётом (15.26), следует:

.

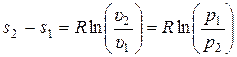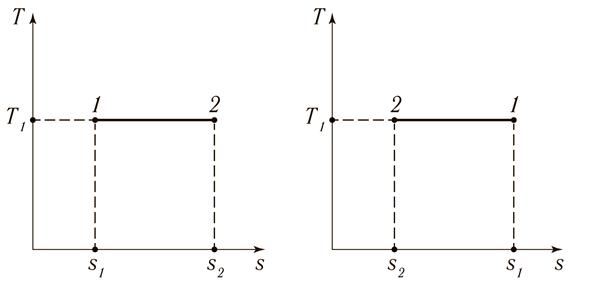
В Ts – координатах изотермический процесс изображается горизонтальной линией, рис. 15.6.

а) б)

Рис. 15.6. Изотермический процесс 1 – 2 в Ts – координатах:

а) с подводом теплоты (расширение газа); б) с отводом теплоты (сжатие газа)