Политропный процесс

Условие, определяющее политропный процесс, записывается в виде:

р υⁿ = const, (15.44)

где р и υ – параметры состояния системы в ходе политропного процесса: абсолютное давление и удельный объём соответственно, Па, м³,кг; n – показатель политропы (безразмерная постоянная величина, значение которой может находится в интервале от –∞ до +∞).

Условие (15.44) говорит о том, что в ходе всего политропного процесса произведение давления газа на его удельный объём в степени n остаётся постоянным. В частности, для любой промежуточной точки политропного процесса можем записать:

р υⁿ = 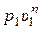, (15.45)

где р₁ и υ₁ – значения давления и удельного объёма в начале процесса, Па, м³/кг.

Из (15.45) можно получить уравнение политропного процесса вида:

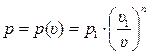, (15.46)

где р(υ) – обозначает функциональную зависимость давления от удельного объёма в политропном процессе, Па.

Связь между параметрами состояния в политропном процессе устанавливается с помощью уравнения состояния идеального газа. Запишем это уравнение для начального и конечного состояния газа точек 1 и 2:

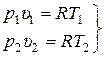. (15.47)

Разделим обе части (15.47) друг на друга:

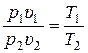. (15.48)

Записав (15.45) для конечного состояния, получаем:

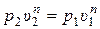, (15.49)

или

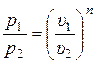, (15.50)

или

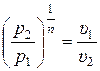. (15.51)

Подставляя (15.50) в (15.48), получаем:

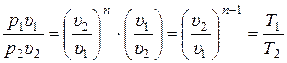. (15.52)

Подставляя (15.51) в (15.48), получаем:

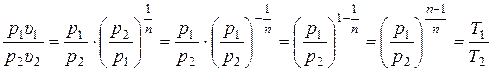. (15.53)

Исходная система уравнений (14.6) с дополнительным условием для политропного процесса имеет вид:

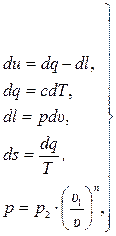(15.54)

где с_n – по определению удельная истинная теплоёмкость политропного процесса с показателем политропы n (неизвестная пока величина),
Дж/(кг∙К).

В результате интегрирования третьего уравнения с учётом последнего условия получаем формулу для удельной работы политропного процесса:

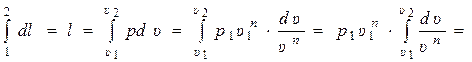
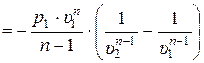. (15.55)

В результате преобразования (15.55) с учётом (15.51) и уравнения состояния идеального газа, получаем следующие формулы:

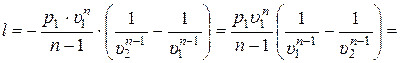
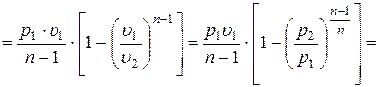
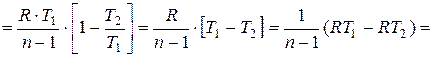
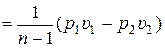. (15.56)

В результате интегрирования первого уравнения в (15.54) получаем:

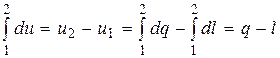
или

q = (u₂ – u₁) + l. (15.57)

Из (15.57), учитывая (15.56), формулу Майера и свойство идеального газа (10.16), получаем формулу для удельной теплоты политропного процесса:

q = (u₂ – u₁) + l = с_υ · (Т₂ – Т₁) + =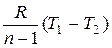

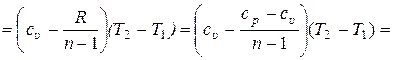
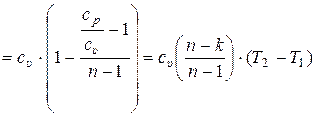, (15.58)

где с_υ – удельная теплоёмкость газа при постоянном объёме, Дж/(кг · К);
n – показатель политропы; k – показатель адиабаты.

Сравнивая формулу (15.58) с определением истинной теплоёмкости политропного процесса 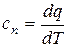(второе уравнение в (15.54)) получаем формулу для вычисления с_υ:

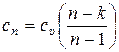. (15.59)

Формула (15.59) справедлива, так как очевидно, что при таком значении с_υ после интегрирования второго уравнения в (15.54) получается формула (15.58), которая вытекает из первого закона термодинамики.

После интегрирования четвёртого уравнения в (15.54) получаем формулу для вычисления изменения энтропии газа в политропном процессе:

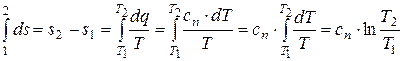. (15.60)

Политропный процесс является обобщающим термодинамическим процессом для идеального газа. Он, в частности, охватывает всю совокупность основных термодинамических процессов, что показано в табл. 15.1.

Таблица 15.1

Значение показателя политропы n для основных термодинамических