Изобарный процесс

Условие, определяющее этот процесс: р = const или dp = 0.

В pυ-координатах изображается горизонтальными линями на рис. 15.3.

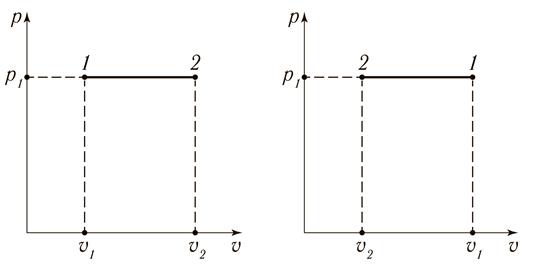
а) б)

Рис. 15.3. Изобарный процесс 1 – 2 в р υ-координатах:

а) с увеличением удельного объёма (расширение); б) с уменьшением удельного объёма (сжатие)

Соотношение между параметрами состояния в ходе изобарного процесса определяется из уравнения состояния идеального газа. Запишем его для точек 1 и 2 – начала и конца изобарного процесса:

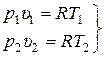. (15.8)

Разделив левые и правые части (15.1) друг на друга получаем:

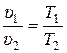. (15.9)

Равенство (15.9) показывает, что в изобарном процессе отношение удельных объёмов равно отношению температур.

Исходная система уравнений (14.6) с дополнительным условием для изобарного процесса имеет вид:

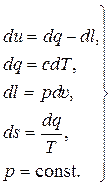(15.10)

Благодаря последнему в (15.10) условию неизвестная в общем случае истинная удельная теплоёмкость с становится известной (из справочника) удельной теплоёмкостью с_р при постоянном давлении. В результате в системе (15.3) число неизвестных функций становится равным числу независимых уравнений, и система становится однозначно разрешаемой.

В результате интегрирования второго уравнения в (15.10) получаем:

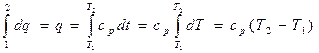. (15.11)

В результате интегрирования третьего уравнения получаем:

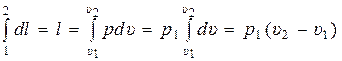. (15.12)

В результате интегрирования первого уравнения получаем:

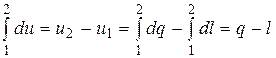. (15.13)

В результате интегрирования четвёртого уравнения получаем:

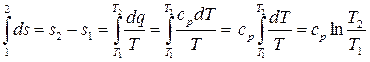. (15.14)

Выводы:

1) Из (15.13) с учётом (15.12) и того, что р₁ = р₂, следует:

q = u₂ – u₁ +l = u₂ – u₁ +p₁ · (υ₂ – υ₁) = u₂ – u₁ +p₂ υ₂ – p₁ υ₁ =

= (u₂ +p₂ υ₂) – (u₁ + p₁ υ₁) = i₂ – i₁, (15.15)

где i₁ и i₂ – удельные энтальпии газа в начале и конце изобарного процесса, Дж/кг.

Формула (15.15) показывает, что теплота в изобарном процессе расходуется на изменение удельной энтальпии системы. (В то время как в изохорном – на изменение удельной внутренней энергии).

С учётом (15.11) вместо (15.15) можем записать:

i₂ – i₁ = с_р (Т₂ – Т₁). (15.16)

При известной с_р выражение (15.16) позволяет построить таблицы для удельной энтальпии, как функции состояния.

2) Используя уравнение идеального газа из (15.12) получаем:

l = р₁ · (υ₂ – υ₁) = p₂ υ₂ – p₁ υ₁ = RT₂ – RT₁ = R · (T₂ – T₁). (15.17)

Рассмотрим далее случай, когда (Т₂ – Т₁) = 1, К. Тогда из (15.17) будем иметь:

l = R · 1, Дж/кг. (15.18)

Равенство (15.18) показывает, что газовая постоянная численно равна работе одного килограмма газа в изобарном процессе при увеличении его температуры на один градус.

3) Из (15.14) следует, что изобарный процесс в T s-координатах является логарифмической кривой, рис. 15.4.

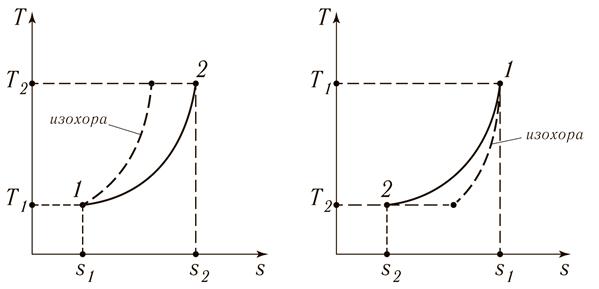
а) б)

Рис. 15.4. Изобарный процесс 1 – 2 в Ts – координатах:

а) с подводом теплоты; б) с отводом теплоты

На рис. 15.4 для качественного сравнения в том же диапазоне температур пунктирной линией изображена изохора, которая идёт круче изобары.