Уравнение Клапейрона
В 1834 году французским физиком Клапейроном путём обобщения уже имеющихся экспериментальных данных было получено уравнение состояния идеального газа следующего вида [4]:
p υ = R T, (1)
где р, υ и Т – основные термодинамические параметры состояния – абсолютное давление, удельный объём и абсолютная температура соответственно, Па, м3/кг, К; R – газовая постоянная, имеющая своё постоянное значение для каждого конкретного газа, Дж/(кг∙К).
Величина R по смыслу является коэффициентом пропорциональности в линейной зависимости произведения (p υ) от T. Значение R определяется экспериментальным путём.
Французский учёный Клапейрон с 1820 по приблизительно 1830 год жил и работал в Санкт-Петербурге. Он преподавал в Институте инженеров путей сообщения и руководил кафедрой прикладной механики.
Примечание:
Уравнение состояния идеального газа (уравнение Клапейрона) характеризует связь между параметрами состояния p, υ и Т. Оно выводится на базе следующих экспериментальных данных [4].
В 1802 году экспериментально была установлена зависимость между объёмом газа и его температурой при условии, что давление газа остается постоянным. Эта зависимость называется законом Шарля – Г.Люсака:
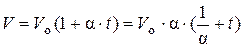, при р = const, (1)
где р – абсолютное давление газа, Па; V – объём, занимаемый газами, м3; Vo – объём, который занимает рассматриваемый газ при температуре 0 оС, м3; t – температура газа, оС; α – среднее значение температурного коэффициента объёмного расширения в интервале температур от 0 до t оС,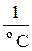 
.
Экспериментально установлено, что
.
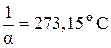Если обе части выражения (1) разделить на массу М, кг. Получим зависимость для удельного объёма υ, м3/кг, этого газа:
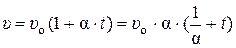, при р = const, (2)
где υо – значение удельного объёма газа при 0 оС, м3/кг.
Также из экспериментов известна зависимость между давлением газа и его температурой при условии, что объём газа остаётся постоянным:
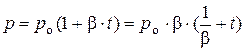, при υ = const, (3)
где ро – давление, которое имеет рассматриваемый газ при температуре 0 оС, Па; β – среднее значение температурного коэффициента давления в интервале температур от 0 до t оС, причём β = α, .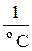
График линейной зависимости р(t) (3) представлен на рис. 1.
Рис. 1. График линейной зависимости (3)
Продолжить график на рис. 1 влево далее точки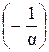 
невозможно, так как абсолютное давление газа не может иметь отрицательных значений по своему определению.
Введём обозначение:
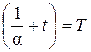, (4)
где Т – абсолютная температура, измеряемая в градусах Кельвина (К), шкала которой строится на базе температурной шкалы Цельсия путём переноса начала отсчёта в точку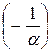 
= – 273,15 °С.
Таким образом, нуль отсчёта абсолютной температуры расположен при температуре – 273,15 оС, то есть сдвинут относительно нуля градусов Цельсия влево на величину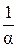 
.
Нулевая точка отсчёта по шкале абсолютной температуры называется абсолютным нулем.
Абсолютный нуль (Т = 0 К) является самой низкой и «холодной» из всех температур. Экспериментально установлено, что охладить любое тело ниже абсолютного нуля невозможно.
С учётом (4) экспериментальные зависимости (2) и (3) примут вид:
υ = υо ∙ α ∙ Т = a ∙ Т, при р = const, (5)
р = ро ∙ α ∙ Т = b ∙ Т, при υ = const, (6)
где a и b – размерные константы, не зависящие от Т, a = υо ∙ α и b = ро ∙ α.
График линейной зависимости (6) р(Т) приведён на рис. 2.
Рис. 2. График линейной зависимости (6) р(Т)
Задолго до обнаружения зависимостей (1) и (3) в 1662 году была получена экспериментальная зависимость между давлением газа р и его удельным объёмом υ при условии, что температура Т остаётся постоянной. Эта зависимость называется законом Бойля-Мариотта [4]:
р ∙ υ = С, при Т = const, (7)
где С – постоянная величина, значение которой не зависит от р и υ, Дж/кг.
Для определения уравнения состояния идеального газа, с учётом (5) – (7), необходимо определить, как зависит от температуры Т произведение давления газа р на его удельный объём υ в общем случае, когда одновременно могут изменяться все три параметра состояния р, υ и Т. То есть требуется определить вид функции f(T), которая равна:
f(T) = f[p(T), υ(T)] = p(T) ∙ υ(T). (8)
Вычислим по (8) производную от f по Т, как производную от сложной функции f[p(T), υ(T)]:
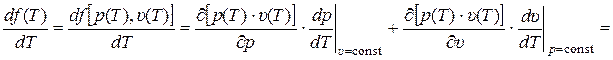
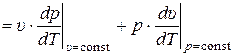. (9)
Из (5) и (6) получим:
, 
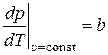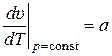. (10)
Подставляя (10) в (9) получаем:
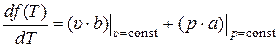. (11)
Оба слагаемых в правой части (11) не зависят от Т (при изменении Т их значения меняться не будут).
Введём обозначение:
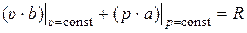. (12)
Очевидно, что R также не зависит от Т. После интегрирования (11) с учётом (12) получаем:
f(T) = R T + A, (13)
где А – постоянная интегрирования, значение которой можно определить с помощью (6).
Из (6) следует, что при Т = 0 значение р = 0, при условии, что
υ = const. Для этого случая из (8) и (13) следует:
f(T) = p(T) ∙ υ(T) = 0 ∙ υ(T) = R ∙ 0 + А, т.е. А = 0. (14)
Докажем, с использованием (7), что R также не зависит от р и υ. Очевидно, что в случае когда температура Т принимает любое конкретное значение Tconst, то одновременно должны выполняться равенства (7) и (8):
р ∙ υ = В, при Т =Тconst, (15)
р ∙ υ = R ∙ Тconst, (16)
где В – некоторая размерная константа, Дж/кг.
Из (15) и (16) следует, что:
В = R ∙ Тconst или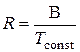 
. (17)
В (17) правая часть не зависит от р и υ при любых значениях Tconst, а значит от р и υ не зависит и R.
Таким образом, окончательно уравнение состояния идеального газа имеет вид:
р ∙ υ = R ∙ Т, (18)
где R – называется газовой постоянной, которая имеет для каждого газа своё постоянное значение, Дж/(кг∙К).
В 1874 году Менделеев преобразовал уравнение (18) к более удобному для многих расчётов виду. Для этого он привлёк дополнительные экспериментальные данные, относящиеся к закону Авогадро, точнее – к следствию из закона Авогадро для одного киломоля идеального газа при нормальных условиях (при температуре t = 0 °С и давлении р = 1 атм = 760 мм рт. ст.=
= 101325 Па).
Прежде чем сформулировать это следствие рассмотрим подробнее содержание и назначение понятия моль или киломоль (1 кмоль = 10 3 моль).
Дата добавления: 2015-03-19; просмотров: 1816;