Закон Авогадро
Закон Авогадро был открыт экспериментальным путём в 1811 году и напрямую с числом Авогадро не связан. Формулируется он следующим образом.
При одинаковых давлениях и одинаковых температурах в равных объёмах различных идеальных газов содержится одинаковое число молекул, или, что то же самое, при одинаковых давлениях и одинаковых температурах моль различных идеальных газов занимает одинаковый объём.
Опытным путём установлено, что при нормальных условиях (н.у. То = 273,15 К и ро = 1 атм = 101325 Па) один киломоль любого идеального газа занимает объём 22,4136 ≈ 22,4 м3. Соответственно один моль будет занимать объём Vo = 22,4 · 10–3 м3.
Этот факт можно рассматривать, как следствие из закона Авогадро для н.у.
2.4. Уравнение Клапейрона – Менделеева
Как уже отмечалось (п. 2.1 данного приложения), путём обобщения экспериментальных данных было получено уравнение состояния идеального газа (1). Учитывая определение удельного объёма его можно переписать в виде:
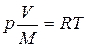 или р V = M R T, (1)
или р V = M R T, (1)
где V – объём газа, м3; M – масса газа, кг.
Соотношение (1) справедливо всегда, в частности, оно будет выполняться для одного киломоля некоторого идеального газа, находящегося при нормальных условиях. Для такого случая, исходя из (1), можно записать:
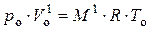 , (2)
, (2)
где ро и То – нормальные давление и температура соответственно
ро = 101325 Па, То = 273,15 К;  – объём, который занимает один киломоль идеального газа при н.у.
– объём, который занимает один киломоль идеального газа при н.у.  = 22,4 м3; М1 – масса одного киломоля газа, кг.
= 22,4 м3; М1 – масса одного киломоля газа, кг.
Значение массы одного киломоля (103 молей) газа определяется
(см. п. 2.2 формулу (2)) следующим образом:
М1 = μ · 1 · 103, (3)
где μ – молярная масса газа, кг/моль.
Подставляя (3) в (2) получаем:
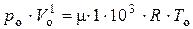 или
или 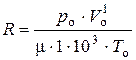 . (4)
. (4)
Подставляя в (4) известные численные значения для ро,  и То, получаем:
и То, получаем:
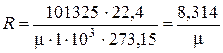 , Дж/(кг·К). (5)
, Дж/(кг·К). (5)
Размерность у числа 8,314, стоящего в числителе (5) Дж/(моль·К). Это число обозначается буквой Rμ, Дж/(моль·К), и называется универсальной газовой постоянной.
С учётом такого обозначения вместо (5) можно записать:
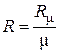 , Дж/(кг·К). (6)
, Дж/(кг·К). (6)
Формула (6) позволяет определить значение газовой постоянной R для любого газа или газовой смеси, не прибегая к экспериментам, так как μ всегда известна.
Подставляя (6) в уравнение идеального газа (см. п.2.1 формула (1)) окончательно получаем уравнение состояния идеального газа в виде формулы Менделеева – Клапейрона:
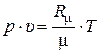 . (7)
. (7)
Дата добавления: 2015-03-19; просмотров: 1017;
