Метод середньої ковзної
Прогнозування на основі середнього значення перемінної використовує інтервал, що задається користувачем для розрахунку середнього значення (за замовченням - 3). На основі ряду первинних даних формується нових ряд із середніх, які обчислюються по вказаному інтервалу вхідних даних з поступовим зміщенням інтервалу по ряду на одну позицію.
Приклад 4.3. Виконати розрахунки прогнозних даних з продажів підприємства на два періоди вперед за допомогою методу середньої ковзної з варіюванням інтервалу – 3; 5; 2. Первинні дані взяти з прикладу 4.2.
Виконання. СтрічкаДанные → група Анализ→ кнопка Анализданнях→ у списку обрати Скользящее среднее → ОК → заповнення полів іде аналогічно попередньому прикладу (метод експоненційного згладжування).
Результати роботи надані на рис. 4.9. Візуально можна відразу оцінити ступінь відповідності прогнозних і фактичних даних, а таблиця дає конкретний прогноз і стандартне відхилення по кожному об'єкту. У порівнянні з попереднім методом на графіку (рис. 3.35) бачимо більш плавну криву і прогноз на два місяці вперед цілком реальний.
| Прогноз за методом середньої ковзної | |||||
| к=3 | Станда-ртні по-хибки | к=2 | Станда-ртні по-хибки | к=5 | Станда-ртні по-хибки |
| #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д |
| #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | |
| #Н/Д | 3,04 | #Н/Д | #Н/Д | ||
| #Н/Д | 4,92 | #Н/Д | #Н/Д | ||
| 6,608 | 5,22 | 132,2 | #Н/Д | ||
| 6,586 | 2,69 | #Н/Д | |||
| 5,288 | 1,12 | 138,2 | #Н/Д | ||
| 1,991 | 1,8 | 142,4 | #Н/Д | ||
| 2,396 | 1,8 | 144,2 | 6,76 | ||
| 4,599 | 3,55 | 146,6 | 5,879 | ||
| 4,329 | 4,32 | 148,2 | 5,292 | ||
| 9,937 | 7,49 | 8,811 |
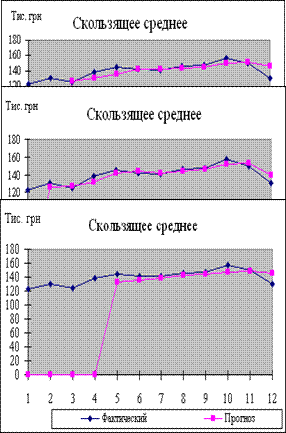
Рисунок 4.9 - Графіки та таблиця фактичних та прогнозних даних за методом середньої ковзної при варіюванні величини інтервалу
Завдання для самостійної роботи.Продовжити приклад для самостійної роботи й включити в нього прогноз за методами експоненційного згладжування й середньої ковзної.
Дата добавления: 2014-12-16; просмотров: 1136;
