Багатофакторна регресія
У реальній дійсності всі економічні процеси взаємопов’язані і часто потрібно визначити ступінь такого зв'язку і вплив на майбутні періоди. Тобто прогнозування повинно йти з урахуванням впливу найбільше істотних факторів. Природно, що для такого прогнозування потрібний більш великий статистичний матеріал.
Послідовність робіт при використанні метода багатофакторної регресії:
1. Збирання статистичних даних та оцінка їх з метою відсіювання випадкових вимірювань. Дані по всіх показниках повинні відповідати нормальному закону розподілу:
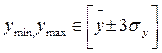 , (4.1)
, (4.1)
де: 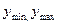 - мінімальне й максимальне значення показника відповідно,
- мінімальне й максимальне значення показника відповідно,
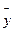 - величина середнього значення показника,
- величина середнього значення показника,
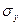 - середнє квадратичне відхилення показника.
- середнє квадратичне відхилення показника.
2. Потрібно дотримуватися статистичної однорідності даних показників, тобто мінливість показників стосовно свого середнього значення не повинна бути занадто високою. Виконання даної вимоги перевіряється за допомогою коефіцієнта варіації Vy. Коефіцієнти варіації показників не повинні перевищувати 33%:
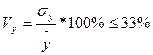 . (4.2)
. (4.2)
Таким чином, стартовою точкою для аналізу даних різних показників, що потрібно включити до моделі та підбору підходящої статистичної моделі є оцінка середнього, стандартних помилок, довірчих рівнів і т. ін., які можна одержати за допомогою методів описової статистики, що є у пакеті аналізу Microsoft Excel.
Необхідно з’ясувати наявність і тип зв’язку між факторами, обраними для моделювання. Між факторними показниками може бути функціональний зв’язок, тоді є чітко визначена формула для розрахунків і факторний аналіз не потрібний, між факторами може не бути зв’язку і регресійний аналіз теж не потрібний. Тільки в разі наявності зв’язків, які не мають чіткого формульного опису, можна використовувати методи багатофакторного аналізу. Наявність зв’язків між факторами та ступінь їх щільності можна оцінити за допомогою коефіцієнта кореляції. Лінійний коефіцієнт кореляції (r) змінюється в межах від -1 до +1. Інтерпретація вихідних значень коефіцієнта кореляції надана в таб. 4.2.
Таблиця 4.2 - Оцінка лінійного коефіцієнта кореляції
| Значення лінійного коефіцієнта кореляції | Характер зв'язку | Інтерпретація зв'язку |
| 0<r<1 | Прямий | Зі збільшенням факторного показ-ника збільшується результативний |
| -1<r<0 | Зворотний | Зі збільшенням факторного показ-ника зменшується результативний |
| r=1 | Функціональний | Кожному значенню факторного показника відповідає одне значення результативного |
| r<½±0,3½ | Відсутній | |
| ½±0,3½£ r£½±0,5½ | Слабкий | |
| ½±0,5½£ r£½±0,7½ | Помірний | |
| ½±0,7½£ r£½±1,0½ | Сильний |
Найкращій результат, коли між факторами є зв’язок, який не перевищує за модулем 0.7; 0.8:
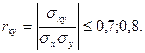 (4.3)
(4.3)
де: 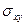 - середнє квадратичне відхилення між факторним і результативним показниками,
- середнє квадратичне відхилення між факторним і результативним показниками,
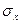 - середнє квадратичне відхилення факторного показника,
- середнє квадратичне відхилення факторного показника,
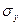 - середнє квадратичне відхилення результативного показника.
- середнє квадратичне відхилення результативного показника.
У випадку наявності великої кількості факторів із слабкими зв’язками можна їх згрупувати й об’єднати в асоційовані групи (замінити одним фактором) з більш тісним зв’язком з змінною, що прогнозується. Таким способом можна зменшити кількість факторів, що аналізуються.
Знак коефіцієнта кореляції вказує на напрямок зв’язку факторів: плюс - прямий зв’язок, мінус – зворотний.
Після відбору факторів можна переходити безпосередньо до використання методу регресії і побудови моделі.
Приклад 4.5. Необхідно спрогнозувати обсяг продажів підприємства на два наступних періоди, якщо відомі продажі за попередні 12 періодів (У), кількість пунктів обслуговування клієнтів (Х1), витрати на рекламу (Х2), вартість одного чеку (Х3) див. рис. 4.12.
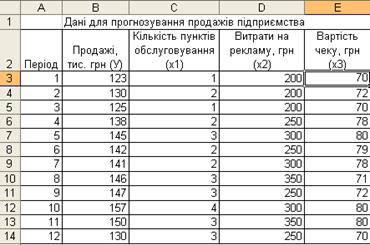
Рисунок 4.12 – Дані для прогнозування продажів підприємства
Для прогнозування необхідно побудувати регресійну модель, яка уявляє собою рівняння виявленого зв'язку між результативним показником і факторами.
Виконання.
1. Оцінка даних на відповідність нормальному закону розподілу: стрічка Данные® група Анализ® кнопка Анализ данных® обрати Описательная статистика®ОК® у діалоговому вікні вказати вхідний діапазон з назвами стовпців В2:Е14® виставити прапорець Метки в первуй строке та Итоговая статистика® селекторна кнопка Выходной интервал® поставити початок вихідного інтервалу G2®ОК.
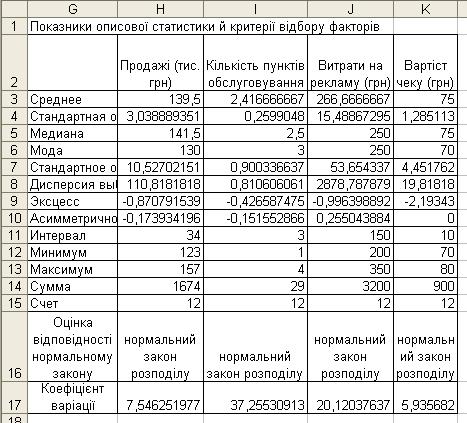 Таблиця з показниками описової статистики показана на рис. 4.13, а два останні рядка - розрахункові дані відповідно формул 4.1 і 4.2.
Таблиця з показниками описової статистики показана на рис. 4.13, а два останні рядка - розрахункові дані відповідно формул 4.1 і 4.2.
Рисунок 4.13 - Показники описової статистики й критерії відбору факторів
Нижче приведені формули клітинок Н16 та Н17:
Н16 - =ЕСЛИ(H13<=(H3+3*H7)&H12>=(H3-3*H7);"нормальний закон
розподілу";"не відповідає нормальному закону розподілу")
Н17 - =H7/H3*100
З рисунку видно, що прогнозний показник та всі фактори підпорядковуються нормальному закону розподілу. Коефіцієнт варіації тільки для кількості пунктів обслуговування трохи перевищує 33%, тому він залишається у розрахунках.
2. Далі виконуємо оцінку наявності зв’язків між показником, що прогнозу-ється, та факторами, що впливають на нього за допомогою лінійного коефіцієнта кореляції (r). Для цього можна використовувати функцію КОРРЕЛ або метод Кореляция з пакету аналізу: стрічка Данные® кнопка Анализ данных® обрати Кореляция® заповнити поля діалого-вого вікна аналогічно попередньому пункту. Результат наведений у таб. 4.3.
Таблиця 4.3 Дані кореляційного аналізу
| Показники | Продажі (тис. грн.) | Кількість пунктів обслуговування | Витрати на рекламу (грн.) | Вартість чеку (грн.) |
| Продажі (тис. грн.) | ||||
| Кількість пунктів обслуговування | 0,829685 | |||
| Витрати на рекламу (грн.) | 0,796713 | 0,690031615 | ||
| Вартість чеку (грн) | 0,698349 | 0,408265792 | 0,532842201 |
Дані другого стовпця таб. 4.3 показують, що найсильніший зв’язок між показниками продажів та кількістю пунктів обслуговування, а найменший – між показниками продажів та вартістю чека. Зв’язок між всіма показниками прямий. Крім того, можна вважати, що всі показники відповідають формулі 4.3.
3. Виконати розрахунки за методом регресії: стрічка Данные® кнопка Анализ данных® обрати Регрессия® заповнити поля діалогового вікна Регрессия (рис. 4.14) ®ОК.
Примітка. Для одержання правильних результатів необхідно, щоб дані розташовувалися у стовпцях і усі фактори були поряд, як вказано на рис. 4.12
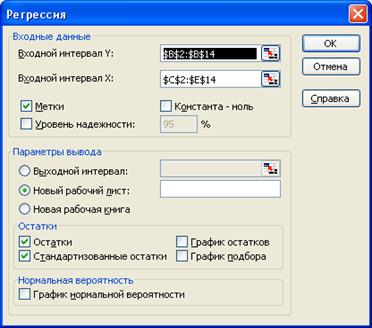
Рисунок 4.14 - Діалогове вікно Регресія
У результаті виконання п. Регресія пакет Excel видає таблиці регресійної статистики, дисперсійного аналізу та таблицю залишків (рис. 4.15).
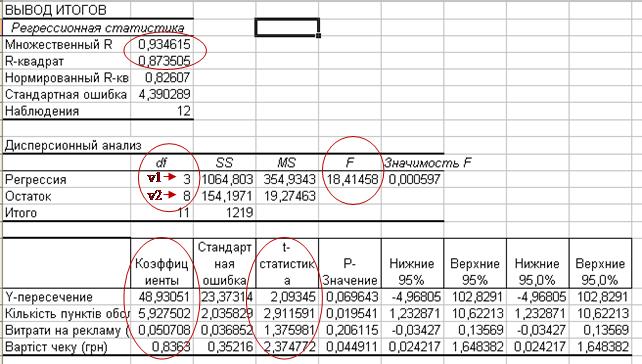 |
Рисунок 4.15 - Таблиці регресійного аналізу
У таблиці регресійної статистики потрібно проаналізувати коефіцієнт детермінації (R2), що показує якою мірою варіація результативного показника обумовлена впливом факторних показників. Таким чином оцінюється вірогідність побудованої регресійної моделі.
Якщо 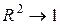 , то лінія регресії точно відповідає всім спостереженням. Коли
, то лінія регресії точно відповідає всім спостереженням. Коли 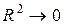 можна стверджувати, що видимий зв'язок між X і Y відсутній.
можна стверджувати, що видимий зв'язок між X і Y відсутній.
Якщо R2 має нечітко виражене граничне значення (наприклад, 0.5), то в таких випадках зручно використовувати критерій Фішера або F-Тест.
У наведеному прикладі R2 дорівнює 0,873505, що свідчить про вірогідність побудованої регресійної моделі. Однак це ще не гарантує невипадковість результату. Необхідно перевірка за критеріями, які можна одержати з таблиці дисперсійного аналізу (F- і t- критерії).
Критерій Фішера або F- критерій для приклада дорівнює 18,41. Його необхідно порівняти з табличним F-критерієм, що вибирається з будь-якого довідника з математичної статистики (додаток Ж). При рівні надійності результату 95% (див. рис. 3.40), та числі ступенів свободи v1=3 і v2=8 (стовпець df таблиці дисперсійного аналізу на рис. 4.15) табличний Fкр = 4,07. Розрахункова величина F значно більше табличної, що свідчить про корисність одержаного регресійного рівняння для прогнозування.
Примітка. Рівень надійності 95% відповідає ймовірності a=0,05. Ступені свободи розраховуються наступним чином: v1 = кількість незалежних факторів; v2 = кількість спостережень або періодів - кількість незалежних факторів - 1.
Другий критерій (t-статистика або критерій Стьюдента) дозволяє оцінити корисність кожного з незалежних факторів для прогнозування ціни. Наприклад, для кількості пунктів обслуговування розраховано t=2,035829, а t-критичне з таблиці при рівні надійності результату 95% і ступені свободи 8 (v= кількість спостережень або періодів - кількість незалежних факторів-1) дорівнює 2,306 (додаток З). Т.к. ½t½>tкр, то відповідний фактор є важливою змінною для оцінки обсягу продажів підприємства. Аналогічно перевіряються інші змінні на статистичну значимість. Всі t для незалежних змінних (факторів), крім витрат на рекламу, більше, чим 2.306, це означає, що вони корисні для прогнозування. Витрати на рекламу у тих обсягах, що затрачувалися підприємством, за t-критерієм не мають значного впливу на обсяги продаж. Але враховуючи тезу «реклама – двигун торгівлі», побудуємо дві моделі з і без вказаного фактора і перевіримо їх.
Модель побудована за допомогою стовпця Коефіцієнти з урахуванням всіх факторів – у=5,93*х1+0,05*х2+0,84*х3+48,93;
без витрат на рекламу - у=5,93*х1+0,84*х3+48,93,
де х1, х2, х3 – конкретні значення факторів, які можуть визначатися різними способами: розрахунковими, прогнозування, будь-які інші.
Виставлені прапорці на рис. 3.40 у розділі залишки надають можливість порівняти фактичні й розрахункові дані. Для наочності додамо до одержаної таблиці фактичні дані та дані за сформованою повною та скороченою моделлю (таб. 4.4).
Таблиця 4.4 ВИВЕДЕННЯ ЗАЛИШКІВ та розрахунки за моделями
| Період | Продажі (тис. грн.) | Прогнозне зна-чення продажів (тис. грн.) | Залишки | Стандартні залишки | Повна модель | Модель без витрат на рекламу |
| 123,54 | -0,54 | -0,14 | 123,66 | 113,66 | ||
| 131,14 | -1,14 | -0,30 | 131,27 | 121,27 | ||
| 123,54 | 1,46 | 0,39 | 123,66 | 113,66 | ||
| 138,69 | -0,69 | -0,19 | 138,81 | 126,31 | ||
| 148,83 | -3,83 | -1,02 | 148,92 | 133,92 | ||
| 139,53 | 2,47 | 0,66 | 139,65 | 127,15 | ||
| 141,23 | -0,23 | -0,06 | 141,31 | 126,31 | ||
| 143,84 | 2,16 | 0,58 | 143,86 | 126,36 | ||
| 139,60 | 7,40 | 1,98 | 139,7 | 127,2 | ||
| 154,76 | 2,24 | 0,60 | 154,85 | 139,85 | ||
| 151,36 | -1,36 | -0,36 | 151,42 | 133,92 | ||
| 137,93 | -7,93 | -2,12 | 138,02 | 125,52 |
Як бачимо, повна модель точніша, тому саме її варто використовувати для прогнозу. Коефіцієнти при змінних показують, на скільки одиниць збільшиться прогнозований показник при зміні фактора на одиницю. Для нашого прикладу при зміні кількості пунктів обслуговування на 1 обсяг продажів збільшиться на 5,93 тис. грн.
Але на основі коефіцієнтів регресії не можна сказати, який з факторних показників найбільш впливає на результативний показник, тому що коефіцієнти регресії між собою не порівнянні, оскільки вони вимірювані різними одиницями. На їхній основі не можна також установити в розвитку яких факторів закладені найбільш великі резерви зміни результативного показника, тому що в коефіцієнтах регресії не врахована варіація факторних показників. Відповіді на ці питання можна одержати, розрахувавши коефіцієнти еластичності: 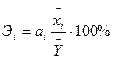 ,
,
де аi- коефіцієнт при хі - показує на скільки одиниць свого виміру зміниться Y, якщо xiзбільшитися на одну одиницю свого виміру, за умови, що всі інші фактори, які включені в модель, впливають на Y, але не варіюють, тобто зафіксовані на рівні свого середнього значення;
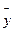 - величина середнього значення показника, що прогнозується;
- величина середнього значення показника, що прогнозується;
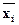 - величина середнього значення фактора.
- величина середнього значення фактора.
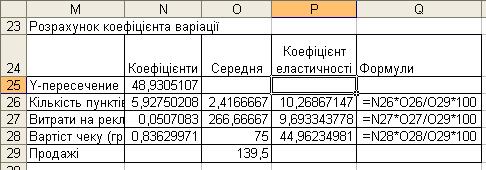 |
Розрахунки коефіцієнтів еластичності наведене на рис. 4.16.
Рисунок 4.16 – Таблиця з розрахунком коефіцієнтів еластичності
Аналіз приватних коефіцієнтів еластичності показує, що за абсолютним приростом найбільший вплив на показник продажів має вартість одного чеку, тобто підвищення вартості чеку на 1% приводить до зростання показника прибутку на 44,96%.
Теоретичні питання оптимізації діяльності підприємства
Фахівці різних сфер у своєї діяльності часто використовують моделювання. У багатьох організаціях для оцінки капітальних вкладень використовують різні моделі фінансових потоків; при призначені цін на товари явно чи неявно використовують моделі еластичності попиту, менеджери активно використовують інвестиційні моделі. Названі задачі вирішуються і на підприємствах ресторанного господарства. Крім того, у підприємств ресторанного господарства є значна кількість задач, які мають багатоваріантні рішення, що залежать від врахування впливу значної кількості змінних факторів. Наприклад, задачі планування загальної діяльності, складання виробничої програми підприємства, раціоналізація транспортних витрат, розподіл робіт на підприємстві та його структурних підрозділах між працівниками та оптимізація витрат на заробітну плату і т. ін.
Помилки у прийнятті рішень за такими складними задачами можуть обернутися значними фінансовими збитками, банкрутством. Сьогоднішня альтернатива підготовки рішень з складних питань – моделювання за допомогою комп’ютера. Помилки тоді залишаються на папері.
Модель [Model, Simulator]— матеріальний об’єкт, система математичних залежностей або програма, що імітують структуру або функціонування досліджуваного об’єкта. Основна вимога до моделі - її адекватність об’єкту.
При прийнятті рішень виконуються наступні етапи:
 |
Процес моделювання при прийнятті управлінських рішень (перші два етапи) наведений на рис. 5.1.
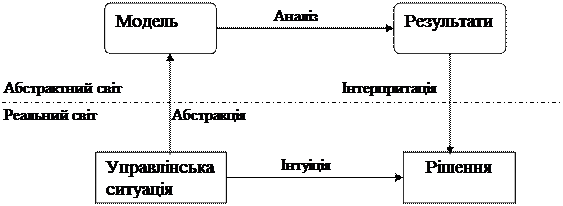 |
Рисунок 5.1 – Процес моделювання при прийнятті управлінських рішень
Процес моделювання, доповнений досвідом та інтуїцією фахівця, дозволяє прийняти більш вдале рішення й багато чому навчитися. Саме тому процес моделювання й прийняття рішень фахівцем неможна розривати.
Примітка. Існує три типи моделей – фізичні (макети літаків, міст…), аналогові (карта основних шляхів є аналоговою моделлю території, кругова діаграма, графік…), символічні або математичні.
Дуже часто при розв’язанні задач виробництва необхідно знайти найкраще значення показника (максимізувати прибуток, мінімізувати витрати…) при наявності обмежених ресурсів. Такі задачі є оптимізаційними задачами.
Відповідно, оптимізаційна модель – детермінована модель прийняття рішень, що містить показник ефективності (цільову функцію), яку необхідно оптимізувати при умові дотримання набору заданих параметрів.
Оптимізація – мінімізація або максимізація цільової функції.
Оптимізаційні моделі складаються з трьох складових.
1. Цільова функція чи критерій оптимізації, показує, у якому змісті рішення повинне бути оптимальним, тобто найкращим. При цьому можливі 3 види призначення цільової функції:
1) максимізація;
2) мінімізація;
3) призначення заданого значення.
2. Обмеженнявстановлюють залежності між змінними. Вони можуть бути як однобічними, наприклад:
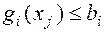 , так і двосторонніми
, так і двосторонніми 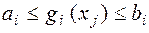 .
.
При рішенні задачі оптимізації за допомогою Ехсеl таке двостороннє обмеження записується у виді двох однобічних обмежень
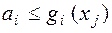 ,
, 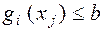
3. Межові умовипоказують, у яких межах можуть бути значення шуканих змінних в оптимальному рішенні.
Рішення задачі, що задовольняє всім обмеженням і межовим умовам, називається припустимим. Якщо математична модель задачі оптимізації складена правильно, то задача буде мати цілий ряд припустимих рішень. Пояснимо це положення. Важливою характеристикою задачі оптимізації є її розмірність, обумовлена числом змінних n і числом обмежень m. Співвідношення цих величин є визначальним при постановці задачі оптимізації. Можливі три співвідношення n<m, n=m, n>m.
1. Якщо n<m, то такі задачі рішення не мають.
2. Якщо n=m, то таке співвідношення n і m — це необхідна умова для рішення системи лінійно-незалежних рівнянь.
3. Якщо n>m, то може бути незліченна безліч значень Xi які задовольняють даній системі рівнянь.
Таким чином, умова n>m — це неодмінна вимога для задач оптимізації. Помітимо, що таку систему рівнянь, для яких n=m, можна розглядати як задачу оптимізації, що має одне припустиме рішення, і вирішувати її як звичайну задачу оптимізації, призначаючи як цільову функцію будь-яку перемінну.
Оптимальне рішення — це найкраще. Але рішення, найкращого у всіх змістах, бути не може. Воно може бути найкращим, тобто оптимальним, тільки в одному, строго встановленому змісті. У реальних обставинах можливі інші варіанти.
Приймаючий рішення повинний абсолютно точно уявляти, у чому полягає оптимальність рішення, тобто за яким критерієм (цільовою функцією) прийняте рішення повинне бути оптимальним.
У загальному випадку за допомогою критерію можна оцінювати якості як бажані (наприклад, прибуток, продуктивність, надійність), так і небажані (загальні витрати, витрата матеріалу, простої устаткування). Тоді в першому випадку прагнуть до максимізації критерію, а в другому — до його мінімізації.
Дата добавления: 2014-12-16; просмотров: 6372;
