Загальна характеристика надбудови Пошук рішення
Надбудова Пошук рішення– компонент, який входить до Excel і призначений для оптимізації моделей при наявності обмежень, у т. ч. моделей лінійного програмування.
Надбудова Пошук рішенняскладається з двох програмних компонентів [4]. Перша програма на Visual Basic транслює з робочого листа інформацію у внутрішнє представлення другої програми. Друга програма у вигляді окремого програмного модуля виконує оптимізацію і повертає знайдене рішення першій програмі. Остання оновлює дані на робочому листі.
Надбудова Пошук рішеннядозволяє обирати метод розв’язання задачі в залежності від її типу. Це наступні методи: нелінійний метод узагальненого знижуючого градієнту (ОПГ), який використовується для розв’язання гладких нелінійних задач; симплекс-метод для розв’язання лінійних задач; еволюційний метод для розв’язання негладких задач.
Надбудова Пошук рішення не підключається до Excel автоматично. Для її підключення необхідно виконати послідовність дій:
М. Файл → к. Параметры→ категорію Надстройки → у полі Управление обрати значення Надстройки Excel → кнопка Перейти → у діалоговому вікні Надстройки установити прапорець Поиск решения → кнопка ОК.
На стрічці Данные у групі Анализ з’явиться кнопка Поиск решения. Для використання методів пошуку рішень необхідно готувати вхідні данні:
1) виділяти діапазон пустих клітинок, у яких програма буде підбирати змінні, що будуть відповідати оптимальному рішенню;
2) розміщати у клітинках розрахункові формули обмежень (ліві їх частини) та у окремих клітинках – праві їх частини;
3) у окремій клітинці вказувати цільову функцію.
Конкретні приклади використання розв’язання оптимізаційних задач будуть розглянуті нижче.
5.4 Задачі оптимального планування.
Розглянемо задачу оптимізації випуску страв у підприємстві харчування.
Приклад 5.1. Підприємство готує 4 види страв (х1, х2, х3, х4). Для виробництва страв використовуються 3 види сировини (максимально можливі добові запаси сировини відповідно 230, 320 і 410 од.). Норми витрат сировини на 1 страву та ціни реалізації кожної страви наведені в таб. 5.2.
Необхідно скласти такий план випуску страв, щоб загальна вартість реалізації була максимальною.
Таблиця 5.2 Дані для розв’язання прикладу 5.1
| Тип сировини | Норми витрат сировини на 1 страву | Запаси сировини на складі (од.) | |||
| Страва 1 | Страва 2 | Страва 3 | Страва 4 | ||
| Сировина 1 | 1,3 | 1,3 | 1,7 | 0,9 | |
| Сировина 2 | 2,1 | 1,1 | 1,7 | ||
| Сировина 3 | 0,9 | 1,4 | 2,1 | ||
| Ціна реалізації 1 порції страви | 12,5 | 21,1 | 9,56 | 11,34 |
Приведена задача ілюструє класичну задачу оптимального планування й розв’язується за допомогою модифікованого симплекс-метода. Математична модель наведена в таб. 5.3.
Таблиця 5.3 Математична модель приклада 5.1
| Математична модель | ||
| Цільова функція | Z=12,5*х1+21,1*х2+9,56*х3+11,34*х4 => max | максимізація ціни реалізації страв |
| Обмеження на ресурси Додатність плана випуску страв | 1,3*x1+1,3*x2+1,7*x3+0,9*x4<=180 | сировина 1 |
| 2,1*x1+1,1*x2+3,0*x3+1,7*x4<=210 | сировина 2 | |
| 0,9*x1+2,0*x2+1,4*x3+2,1*x4<=800 | сировина 3 | |
| {х1,х2,x3,x4}>=0 |
Виконання.
1. Введемо вхідні дані задачі за схемою (рис. 5.3), де В10:Е10 – діапазон змінних, що будуть підбиратися; D12 – цільова функція; А15:А17 – ліві частини обмежень; D15: D17 – праві частини обмежень.
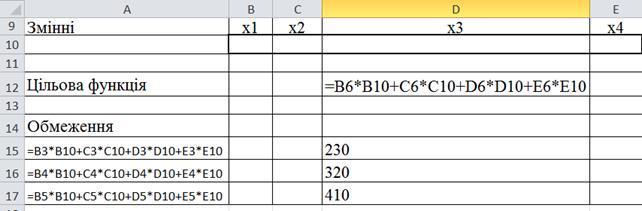
Рисунок 5.3 - Схема розташування на листі змінних, цільової функції та обмежень.
2. Викликати надбудову Поиск решения: стрічка Данные → група Анализ → кнопка Поиск решения → з’явиться діалогове вікно “Поиск решения” (рис. 5.4), у якому потрібно вказати клітинку з цільовою функцією (D12), критерій пошуку – максимум, пусті клітинки для змінних (В10:Е10), обмеження по одному і кнопку Добавить або масивом, як показано на рисунку, обрати метод розв’язання задачі – симплекс-метод, виставити прапорець Сделать переменные без ограничений неотрицательными → кнопка Найти решение.
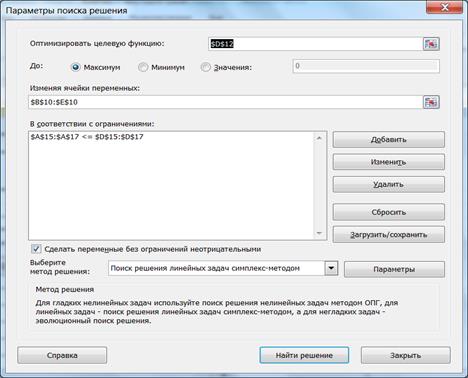
Рисунок 5.4 - Діалогове вікно «Поиск решения»
Примітка. Обмеження можна задавати і у вигляді діапазонів або вводити послідовно. В останньому разі кожне обмеження закінчується кнопкою Добавить для продовження введення наступного обмеження або ОКдля закінчення їх введення.
3. Оцінити одержаний результат й зберегти або відхилити рішення: у вікні Результаты поиска решения, що відкриється, користувач повідомляється про результати пошуку, а на листі Excel з’являються результати обчислень (рис. 5.5). Якщо результати задовольняють, то клацнути кнопку ОК.

| Змінні | х1 | х2 | х3 | х4 |
| 176,9231 | ||||
| Цільова функція | 3733,08 | |||
| Обмеження | ||||
| 194,6153846 | ||||
| 353,8461538 |
Рисунок 5.5 – Вікно Результаты поиска решения та самі результати розрахунків (максимум 1)
Як бачимо з рис. 5.5, виявилося, що доцільно випускати 177 од. Страви 2 і при цьому максимальна вартість реалізації буде складати 3733 грн. (при умові, що всі 177 од. страви будуть реалізовані). Що стосується обмежень на ресурси, то сировина 2 і 3 буде використовуватися не повністтю. Таким чином, одержано суцільно теоретичне рішення, яке назвемо максимум 1.
Якщо необхідно забезпечити випуск всіх страв, з одного боку, й використати всю сировину (має обмежені терміни зберігання), з іншого, то слід змінити тип обмежень з «<=» на «=». У результаті розрахунків зі зміненим типом обмежень одержимо рішення: доцільно випускати Страва 1 - 21 од., Страва 2 - 79 од. Та Страва 4 - 111 од.; максимальна вартість реалізації страв буде складати 3188 грн.; ресурси будуть використані повністтю.
Максимум2
| Обчислені значення випуска страв | ||||
| Страва1 | Страва2 | Страва3 | Страва4 | |
| Цільова функція | ||||
| Обмеження на ресурси | сировина1 | ||
| сировина2 | |||
| сировина3 |
Але одержане рішення не задовольняє умову, що всі страви повинні випускатися (випуск Страва 3 дорівнює 0). Щоб задовольнити цю умову необхідно спочатку розв’язати задачу на мінімум, а потім знайти найбільш підходящий варінт рішення задачі.
При розв’язані задачі на мінімум необхідно змінити прапорець для цільової функції. Відповідно оптимальному рішенню умова на повне використання всіх ресурсів виконана, але тепер недоцільно випускати Страву 1.
Мінімум
| Обчислені значення випуска страв | ||||
| Страва1 | Страва2 | Страва3 | Страва4 | |
| Цільова функція | ||||
| Обмеження на ресурси | сировина1 | ||
| сировина2 | |||
| сировина3 |
Тепер можна переходити до пошуку задовільного рішення для всіх умов. Для цього задача вже розв’язується не на граничні значення (максимум або мінімум), а на прирівнювання цільової функції до конкретного значення, що знаходиться в діапазоні рішення на мінімум та максимум 2 (3090<Z<3188, де Z-цільова функція). Таке рішення назвемо консенсусним, т.к. воно буде оптимальне з точки зору двох обмежень (обов’язковий випуск всіх видів страв та повне використання всіх ресурсів), але не оптимальне з точки зору максимізації вартості реалізації страв. Це пояснюється тим, що багатокритеріальність поставленої задачі входить у суперечність з цільовою функцією на максимум.
Консенсус
| Обчислені значення випуска страв | ||||
| Страва1 | Страва2 | Страва3 | Страва4 | |
| Цільова функція | ||||
| Обмеження на ресурси | сировина1 | ||
| сировина2 | |||
| сировина3 |
В результаті розв’язання задачі вартість реалізації продукції складає 3100 грн., що на 633 грн. менше максимального значення, але при цьому будуть виконані дві умови: будуть випущені всі страви та використані всі наявні ресурси. Таке рішення буде умовно оптимальне.
Щоб визначити вигідність такого рішення для підприємства, необхідно додатково провести аналіз, що краще – одержати менший прибуток від повністю задовільненого попиту клієнтів або переглянути перелік страв. Таку задачу повинен розв’язувати менеджер підприємства.
Дата добавления: 2014-12-16; просмотров: 2396;
