Теорема Гаусса

Рассмотрим поле единичного положительного заряда q.

Окружим заряд сферической поверхностью радиуса r. Поток ФЕ через эту поверхность равен: 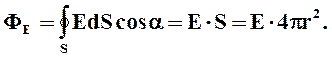1) Во всех точках поверхности 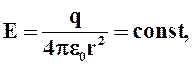т.к. r = const для всех точек среды.

2) a = 0°, cosa = 1. Тогда

Окружим заряд произвольной поверхностью: сколько силовых линий пронизывает сферическую поверхность, столько же их пронизывает произвольную поверхность, т.е. для произвольной поверхности

Если внутри поверхности находится несколько точечных зарядов, то 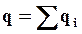и

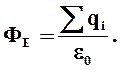
Теорема Гаусса: поток вектора через произвольную замкнутую поверхность, охватывающую заряд, равен величине этого заряда, деленной на электрическую постоянную e₀.

Рассмотрим случай, когда заряды находятся вне замкнутой поверхности.

Каждая силовая линия 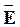пересекает поверхность дважды: один раз она входит в поверхность, второй – выходит из нее. Поэтому

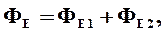
где Ф_Е1 – поток, образуемый входящими линиями (Ф_Е1<0, т.к. a₁>90° и cosa₁<1); Ф_Е2 – поток, образуемый выходящими линиями (Ф_Е2>0, т.к. a₁<90° и cosa₁>1).

Так как 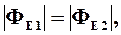то Ф_Е = 0, т.е. вне замкнутой поверхности поток вектора 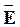равен нулю.

Теорема Гаусса позволяет рассчитывать 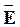и j электростатических полей и в этом смысле эквивалентна закону Кулона. Оба эти закона устанавливают связь зарядов как источников поля с самими характеристиками поля.