Поле двух параллельных бесконечных равномерно заряженных плоскостей
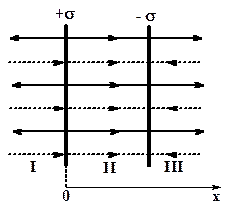
| Для рассматриваемого случая воспользуемся принципом суперпозиции электрических полей. Изобразим линии напряженности положительно заряженной плоскости сплошными линиями, отрицательно заряженной плоскости – пунктирными. Укажем направление силовых линий в областях I, II и III. |
Результирующая напряженность в каждой области по принципу суперпозиции:
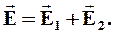
Напряженности, создаваемые каждой плоскостью в отдельности:
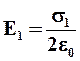 и
и 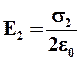 .
.
Из рис. видно, что в области IIвекторы 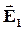 и
и 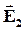 сонапралены и при
сонапралены и при 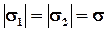
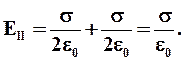
В областях I и III векторы 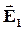 и
и 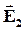 направлены противоположно друг другу, т.е.
направлены противоположно друг другу, т.е. 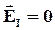 и
и 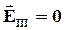 .
.
Найдем разность потенциалов между плоскостями. Обозначим расстояние между ними d и воспользуемся соотношением:


Интегрируя 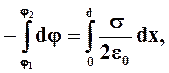
получим 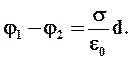
3. Поле бесконечной нити, заряженной с линейной плотностью l
Линейная плотность заряда – заряд, приходящийся на единицу длины:
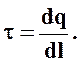
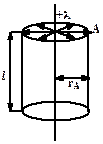
| Для нахождения 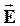 в т. Aудобно выбрать замкнутую поверхность в виде цилиндра. Линии в т. Aудобно выбрать замкнутую поверхность в виде цилиндра. Линии 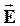 перпендикулярны нити, следовательно, поток вектора перпендикулярны нити, следовательно, поток вектора 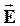 будет только через боковую поверхность цилиндра. будет только через боковую поверхность цилиндра.
|
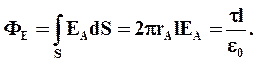
Следовательно,
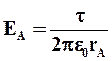 .
.
Разность потенциалов между точками 1 и 2 поля, лежащими на расстоянии r1 и r2 от оси цилиндра:

3. Поле заряженной сферической поверхности
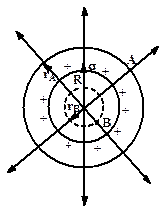
| Проводим вокруг полой металлической сферы сферическую поверхность радиусом rA. Поток вектора через эту поверхность
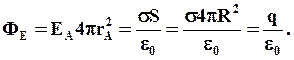 Тогда
Тогда 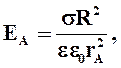 или или 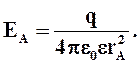
|
Видно, что выражение для 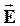 получилось таким же, как и для точечного заряда.
получилось таким же, как и для точечного заряда.
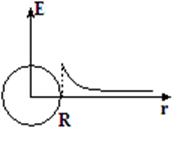
| Внутри сферы, например в т. B, величина 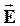 =0, т.к заряд внутри сферы, проведенной через т. B, равен нулю. Величина =0, т.к заряд внутри сферы, проведенной через т. B, равен нулю. Величина  и и 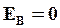 . Напряженность электрического поля меняется как показано на рисунке . Напряженность электрического поля меняется как показано на рисунке
|
Разность потенциалов
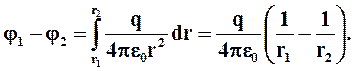
Шар, представляющий собой диэлектрик, может быть внутри равномерно заряжен с объемной плотностью 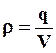 . Поток вектора
. Поток вектора 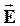 через поверхность радиусом r<R (R – радиус шара) равен
через поверхность радиусом r<R (R – радиус шара) равен 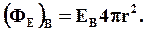 Заряд внутри сферы радиусом rравен:
Заряд внутри сферы радиусом rравен:
 .
.
По теореме Гаусса
 и
и 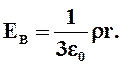
За пределами равномерно заряженного шара выражение для EA будет таким же, как и полученное нами для полой сферы 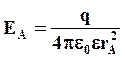 , только величина qбудет равняться rV:
, только величина qбудет равняться rV:

Разность потенциалов для точек, лежащих на расстоянии r>R от центра шара:

и для точек, лежащих на расстоянии r<R от центра шара:
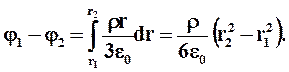
Дата добавления: 2014-12-09; просмотров: 2578;
