Применение теоремы Гаусса
1. Поле бесконечной равномерно заряженной плоскости
Величину заряда, приходящуюся на единицу поверхности, называют поверхностной плотностью заряда s:
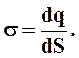

| Пусть плоскость заряжена положительно с поверхностной плотностью заряда +s=const. Из соображений симметрии силовые линии имеют вид прямых, перпендикулярных плоскости и выходящих из положительных зарядов . |
Найдем напряженность в точке A.

| В соответствии с законом Кулона для нахождения величины 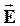 в т. A нужно плоскость разделить на точечные заряды и потом суммировать величины в т. A нужно плоскость разделить на точечные заряды и потом суммировать величины 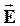 , созданные каждым из этих зарядов. Эта процедура довольно сложная. Теорема Гаусса позволяет решить задачу по отысканию , созданные каждым из этих зарядов. Эта процедура довольно сложная. Теорема Гаусса позволяет решить задачу по отысканию 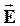 очень просто. Через т. A нужно провести замкнутую поверхность и найти поток очень просто. Через т. A нужно провести замкнутую поверхность и найти поток 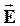 через нее. через нее.
|
Поверхность обычно берут такой, чтобы максимально просто можно было бы вычислить ее площадь. В случае заряженной плоскости этой поверхностью является цилиндрическая, у которой образующая перпендикулярна плоскости. Поскольку линии 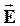 перпендикулярны заряженной плоскости и угол aмежду вектором
перпендикулярны заряженной плоскости и угол aмежду вектором 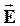 и нормалью к основаниям цилиндра равен нулю, следовательно, cosa=1. Для боковой же поверхности
и нормалью к основаниям цилиндра равен нулю, следовательно, cosa=1. Для боковой же поверхности 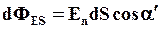 . Угол a’=90°, следовательно, cosa=0 и
. Угол a’=90°, следовательно, cosa=0 и 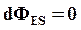 .
.
Итак, общий поток вектора 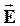 через замкнутую цилиндрическую поверхность
через замкнутую цилиндрическую поверхность  равен сумме потоков через два основания
равен сумме потоков через два основания 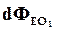 и
и  и потоку через боковую поверхность
и потоку через боковую поверхность  :
:
 где
где  - берем элементарные площадки одинаковой величины.
- берем элементарные площадки одинаковой величины.
Суммарный заряд внутри цилиндра
 .
.
Тогда по теореме Гаусса запишем:

и получаем:
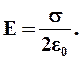
Найдем разность потенциалов поля между точками 1 и 2 на расстоянии x1 и x2 от плоскости. Воспользуемся соотношением  . Векторы напряженности
. Векторы напряженности 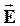 направлены по оси Ox, поэтому:
направлены по оси Ox, поэтому:



откуда получим:
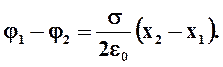
Дата добавления: 2014-12-09; просмотров: 1059;
