Корреляционная функция

Корреляционная функция 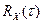стационарного процесса 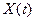также может быть вычислена двумя способами, усреднением по ансамблю (через совместную плотность вероятности) и усреднением одной реализации по времени. Для эргодического процесса оба метода дают один и тот же результат.

Далее мы будем рассматривать только эргодические процессы, для которых можно найти корреляционную функцию по одной реализации. Чтобы вычислить 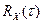для некоторого 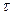, нужно найти среднее значение произведения :

.

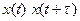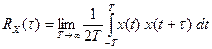(1)

Построить график функции 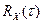можно по точкам, выполнив такое интегрирование для каждого значения 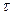из некоторого массива.

Корреляционная функция обладает рядом важных свойств:

1) 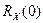– это средний квадрат случайного процесса, поэтому всегда 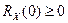; для центрированных процессов (с нулевым средним) эта величина совпадает с дисперсией;

2) при 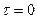корреляционная функция имеет наибольшее значение, в том числе и наибольшее по модулю, то есть 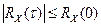при всех ;

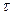3) 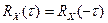, то есть 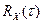– симметричная (четная) функция, это доказывается подстановкой 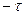вместо 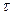в интеграл (1); поэтому можно считать корреляционную функцию только для 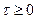, а вторую часть строить симметрично.

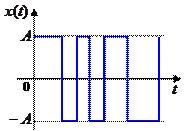
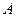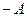В качестве примера приведем корреляционную функцию дискретного сигнала, который переключается между значениями и в случайные моменты времени:

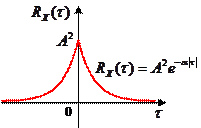
Корреляционная функция имеет вид 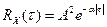, где 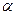– среднее число переключений за 1 с. Заметим, что одна и та же корреляционная функция может соответствовать многих совершенно различным процессам.

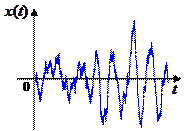
Корреляционная функция не всегда положительна. На следующих рисунках показано изменение ординаты поверхности морского волнения и корреляционная функция этого сигнала (одна из теоретических моделей):

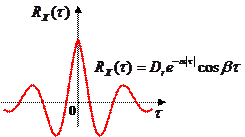
Здесь 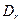– дисперсия волновой ординаты, 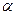– коэффициент затухания и 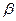– средняя частота волнения.

Заметим также, что чаще всего корреляционная функция убывает по модулю, т.е. чем дальше от нуля, тем меньше значение модуля корреляционной функции (чем больше расстояние между отсчетами, тем меньше связь между ними). Это справедливо не для всех случайных процессов, но для большинства практических ситуаций.