Белый шум

В математике для теоретических исследований иногда удобно использовать математические объекты, которые нереализуемы на практике (например, дельта-функцию). В теории случайных процессов важную роль играет белый шум[5], имеющий равномерную спектральную плотность по всем частотам, то есть, 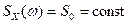. Очевидно, что при этом площадь под кривой спектральной плотности (определяющая средний квадрат процесса) бесконечна, то есть сигнал имеет бесконечную мощность и не может существовать в природе.

Если нет никакой информации о свойствах случайных возмущений, действующих на системы, часто считают, что они приближенно описываются моделью белого шума. Если мы докажем, что даже в этом (наихудшем) случае характеристики системы останутся удовлетворительными, то они будут не хуже и при любой другой случайной помехе.

Корреляционная функция белого шума равна 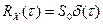. Действительно, преобразование Фурье сразу дает

.

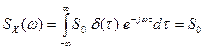Значения такого сигнала отстоящие по времени на любой, сколь угодно малый интервал, некоррелированы. Это означает, что нет никакой зависимости между соседними, сколь угодно близко расположенными друг к другу, отсчетами такого случайного процесса. Корреляционная функция и спектральная плотность белого шума показаны на рисунках:

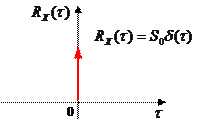
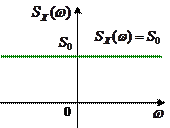
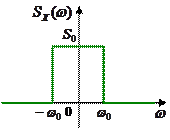
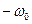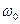Белый шум, как сигнал с бесконечной энергией, невозможно получить на практике. При моделировании его обычно заменяют на белый шум с ограниченной полосой, который имеет равномерный спектр в полосе частот от до , и нулевой вне этой полосы:

.

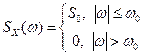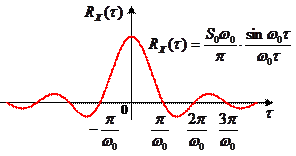
Средний квадрат такого сигнала равен 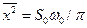, а не бесконечности. Корреляционную функцию можно найти с помощью обратного преобразования Фурье:

.

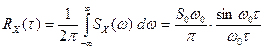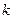Поскольку при любом целом , корреляционная функция равна нулю при всех 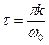, где 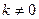– любое целое число, не равное нулю. Это значит, что значения, взятые из такого сигнала в моменты времени 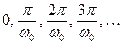, (выборка с периодом ) будут некоррелированы.