Гармонический сигнал

Рассмотрим гармонический сигнал

,

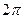где – случайная фаза, равномерно распределенная в интервале от 0 до . Три реализации этого процесса (с разными фазами ) показаны на рисунке:

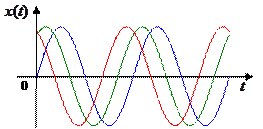
Это тоже случайный процесс, однако его отличие от «классических» случайных процессов состоит в том, что зная (или определив) случайную фазу , мы может вычислить значение этого сигнала при любом 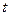. Таким процессы называют квазидетерминированными. Как только фаза определена, процесс становится детерминированным (не случайным).

Использование формулы для усреднения по времени (1) дает

.

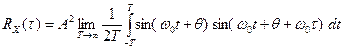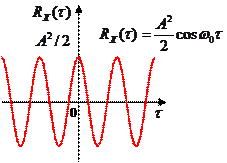
После несложных преобразований (применение формулы произведения синусов и интегрирование), получим .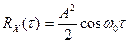

Чтобы найти спектр такого сигнала, вычислим преобразование Фурье для корреляционной функции. По таблицам находим , поэтому

.

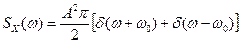Это значит, что спектральная плотность состоит из двух дельта-функций для частот 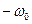и 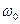, а в остальных точках равна нулю. Действительно, с самого начала было легко догадаться, что вся энергия такого сигнала сосредоточена на одной частоте.