Эргодичность

При первом знакомстве со случайными процессами всегда возникает закономерный вопрос: «Как же изучать случайные процессы на практике?» Дело в том, что во многих случаях мы наблюдаем только одну реализацию из всего ансамбля, и повторить опыт с теми же условиями невозможно.

Исследователи почти всегда предполагают, что длительное наблюдение за одной реализацией случайного процесса позволяет изучить свойства ансамбля, то есть, один элемент ансамбля содержит информацию обо всех остальных элементах. Случайные процессы, обладающие таким свойством, называют эргодическими. Заметим, что только стационарный процесс может быть эргодическим.

С одной стороны, в реальных ситуациях очень сложно доказать эргодичность. С другой – обычно имеет смысл предположить, что процесс эргодический, если нет веских доводов против этого.

Для эргодических процессов по одной реализации можно найти все основные характеристики, заменив усреднение по ансамблю на усреднение по времени. Например, математическое ожидание стационарного случайного процесса можно теоретически найти через его плотность распределения:

.

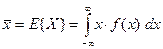Если мы знаем только одну реализацию, можно попробовать оценить среднее значение на интервале , разделив интеграл от функции на ширину интервала:

.

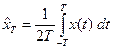Переходя к пределу при (применяя усреднение на бесконечном интервале), получаем оценку среднего значения по одной реализации :

.

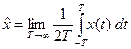Для эргодических процессов это значение совпадает с , которое получено путем усреднения по ансамблю.