Какие бывают распределения?

Существует бесчисленное множество разных распределений, но в технике применяются лишь некоторые из них.

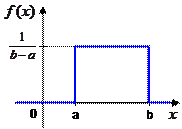
Самое простое – это равномерное распределение. Например, снег в безветренную погоду ложится на плоскую поверхность равномерно – ровным слоем, который имеет одинаковую толщину во всех точках. Обычно предполагается, что ошибка квантования непрерывных сигналов в цифровом компьютере имеет равномерное распределение. Равномерное распределение на интервале 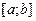описывается плотностью распределения

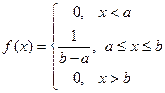
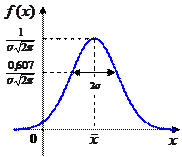
Самое важное распределение в практических задачах – нормальное распределение (распределение Гаусса), для которого график плотности распределения имеет форму колокола:

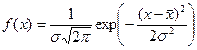
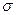Здесь – среднее значение, а – среднеквадратическое отклонение случайной величины. Распределение Гаусса обладает несколькими замечательными свойствами:

1) сумма (и любая линейная комбинация) случайных величин с нормальными распределениями тоже имеет нормальное распределение;

2) если на величину действует множество независимых помех, ее плотность вероятности стремится к нормальному закону;

3) при прохождении случайного сигнала с нормальным распределением через линейную систему сигнал на выходе тоже имеет нормальное распределение.

Если нет никаких теоретических или экспериментальных данных о распределении случайной величины (например, шума измерений), чаще всего предполагают, что это распределение – нормальное.

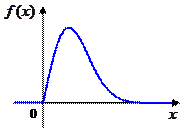
В специальных задачах применяют и другие распределения. Например, установлено, что плотность распределения высот волн при морском волнении определяется законом Рэлея:

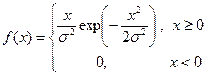
Например, так распределяются высоты волн при морском волнении.

Для моделирования случайных события в компьютерных моделях используют датчики псевдослучайных чисел (они похожи на случайные, но каждое следующее вычисляется по некоторой формуле, использующей предыдущие значения). Большинство датчиков «выдают» равномерно распределенные значения, из которых с помощью математических операций можно получить другие распределения.

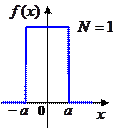
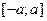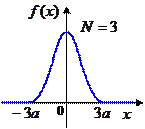
Например, рассмотрим сумму нескольких независимых случайных значений, равномерно распределенных на симметричном интервале . Можно показать, что для суммы двух чисел получится треугольное распределение. Таким образом, складывая два случайных числа, полученных со стандартного датчика с равномерным распределением, мы получим числа с треугольным распределением. Для суммы трех чисел график состоит из кусочков парабол:

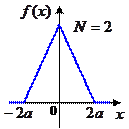
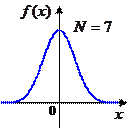
При увеличении 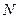график плотности распределения вероятностей становится всё больше похож на «колокол» нормального распределения. Доказано, что при больших 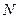распределение суммы 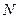чисел действительно стремится к нормальному (на практике часто берут 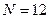). Более того, это справедливо для суммы большого количества независимых случайных величин с любым распределением (не обязательно равномерным).